函数y=−x2(x≥0)y=−x2(x≥0)的反函数的定义域是( )。单项选择题选项:
A. [0,+∞)[0,+∞)
B. [−∞,1][−∞,1]
C. (0,1](0,1]
D. (−∞,0](−∞,0]
查看答案
相关试题
换一换


函数y=−x2(x≥0)y=−x2(x≥0)的反函数的定义域是( )。单项选择题选项:
A.[0,+∞)[0,+∞) B.[−∞,1][−∞,1] C.(0,1](0,1] D.(−∞,0](−∞,0]
答案
函数f(x)的定义域是[0,1],则函数f(2x)的定义域是().
答案
已知函数f(2x)的定义域为(0,1),则函数f(x+1)的定义域为()
A.(0,2) B.(0,1/2) C.(-1,1) D.(1,3)
答案
已知函数f(x)的定义域为[0,1],求函数f(x+a)+f(x-a)(a>0)的定义域.
答案
已知函数ƒ(x)的定义域为R,且满足ƒ(2x)=3x,则ƒ(x)的反函数为()。
A.y=log2x3 B.y=2log3x C.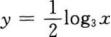 D.
D.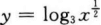
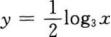 D.
D.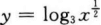
答案
设函数y=f(x)的定义域为(1,2],则f(ax)(a<0)的定义域是()
A.(1/a.2/a] B.[2/a.1/a) C.(a.2a] D.(2/a.a]
答案
已知函数f(x)的定义域为[0,4],则函数φ(x)=f(x+1)+f(x-1)的定义域为____。
答案
已知函数f(x)的定义域为(-∞,+∞),对任意的x,y,有f(x+y))+f(x-y)=2f(x)f(y)成立,且f(0)≠0.求证:
(1)f(0)=1;
(2)函数f(x)是偶函数.
答案
函数f(x)=lg(2x-2)的定义域是 ( )。
A.(0,1) B.(1,2) C.(-∞,1) D.(1,+∞)
答案
若函数ƒ(x)的定义域为[0,1],则ƒ(cosx)的定义域为()。
A.[0,1] B.(-∞,+∞) C.[-π/2,π/2] D.[2kπ-π/2,2kπ+π/2](k∈Z)
答案
热门试题
函数y=1+log2x(x>0)的反函数为()。
函数f(x)=ln(1-2x)的定义域是()
函数f(x)=x2 在定义域内是( )。
已知定义域为R的偶函数f(x)在(-∞,0)上单调递减,且f(2)=0,则满足f(x)≥0的x的取值范围是()
设函数f(x)的定义域为(0,1],则f(sinx)的定义域为()
设函数y=f(ex-1)的定义域为[0,1],则f(x)的定义域是()
函数y=lg(x2-3x+2)的定义域为( )
函数y=ln2x的定义域是
函数y=lg(2-x)的定义域是( )
函数 y=x1/2的定义域是()
函数y=lg(2-x)的定义域是()
函数y=lg(x2-x-2)的定义域为()。
函数y=lg(x2-3x+2)的定义域为()。
若函数y=f(x)的定义域是[-1,1],那么f(2x-1)的定义域是()。
函数y=lg(x2-1)的定义域是
函数y=log2(x+1)的定义域是()
函数y=-2x+1在定义域R内是()
函数f(x)=log2(x+1)的定义域为()
若函数f(x+1)的定义域是[-1,1],则函数f(x)的定义域是().
若不等式x2-x≤0的解集为M,函数?(x)=In(1-|x|)的定义域为N,则M∩N为().?



 使用微信扫一扫登录
使用微信扫一扫登录