(拉格朗日中值定理)下列函数在区间[-1,1]上满足拉格朗日中值定理条件的是
查看答案
相关试题
换一换


(拉格朗日中值定理)下列函数在区间[-1,1]上满足拉格朗日中值定理条件的是
答案
下列函数在给定区间上满足拉格朗日中值定理条件的是()
A.y=sinx,[0,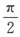 ] B.y=
] B.y= ,[-2,2] C.y=
,[-2,2] C.y=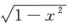 ,[0,2] D.y=
,[0,2] D.y=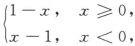 [-1,1]
[-1,1]
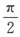 ] B.y=
] B.y= ,[-2,2] C.y=
,[-2,2] C.y=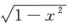 ,[0,2] D.y=
,[0,2] D.y=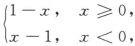 [-1,1]
[-1,1] 答案
下列函数在[1,e]上满足拉格朗日中值定理条件的是()。
A.1/(1-x) B.lnx C.1/(1-lnx) D.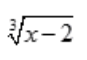
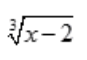
答案
函数f(x)=e2x在区间[0,1]上满足拉格朗日中值定理结论的ξ=().
答案
拉格朗日中值定理中函数应满足的条件是下面哪几项(? ? )
答案
拉格朗日中值定理也叫微分中值定理
答案
设函数在可导,取定,在区间上用拉格朗日中值定理,有,使得,这里的是的函数()
A.正确 B.错误
答案
拉格朗日中值定理有几个条件?
答案
设函数f(x)=x2+px+q,则函数在[a,b]上满足拉格朗日中值定理结论的ξ=().
答案
罗尔中值定理是拉格朗日中值定理的特殊情况。()
A.错误 B.正确
答案
热门试题
若函数在[1,2]上满足拉格朗日中值定理的条件,则=/ananas/latex/p/8341/ananas/latex/p/374
试分别叙述罗尔中值定理和拉格朗日中值定理。若以S(x)记由(a,ƒ(a)),(b,ƒ(b)),(x,ƒ(x))三点组成的三角形面积,试对S(x)应用罗尔中值定理证明拉格朗日中值定理。
试分别叙述罗尔中值定理和拉格朗日中值定理。若以S(x)记由(a,(a)),(b,(b)),(x,(x)))三点组成的三角形面积,试对S(x)应用罗尔中值定理证明拉格朗日中值定理。
f(x)在闭区间[0,c]上连续,其导函数f’(x)在开区间(0,c)内存在且单调递减,f(0)=0。(1)结合题干简述拉格朗日中值定理的内容并证明;(2)运用拉格朗日中值定理证明不等式f(a+b)≤f(a)+f(b),其中常数a,b满足条件0≤a≤b≤a+b≤c。
柯西中值定理相当于把拉格朗日中值定理中的那条曲线弧用参数方程来表示
微分中值定理是一系列中值定理总称,是研究函数的有力工具,其中最重要的内容是()定理,可以说其他中值定理都是拉格朗日中值定理的特殊情况或推广
拉格朗日中值定理的结论和微分的近似计算公式没有区别
叙述并证明拉格朗日微分中值定理,并简述拉格朗日微分中值定理与中学数学内容的联系。
下列函数在给定区间上满足罗尔中值定理条件的是()
下列函数在指定区间上满足罗尔中值定理条件的是()。
在区间[-1,1]上,下列函数不满足罗尔中值定理条件的是()
下列函数中,在区间[-1,1]上不满足罗尔中值定理条件的是()。
设f(x)在闭区间[0,c]上连续,其导数f′(x)在开区间(0,c)内存在且单调减少,f(0)=0,试应用拉格朗日中值定理证明不等式f(a+b)≤f(a)+f(b)其中a,b满足条件0≤a≤b≤a+b≤c.
拉格朗日定理实际上是带有拉格朗日余项的泰勒公式的特殊情形。
函数 在区间 上是否满足罗尔定理的条件?_
下列函数在区间[-1,1]上满足罗尔定理条件的是( )。
拉格朗日多项式可以表示成拉格朗日基函数的线性组合
拉格朗日基函数的和为
在区间[-2,2]上,下列函数中不满足罗尔定理条件的是()。
使函数 满足罗尔定理的区间是( )。



 使用微信扫一扫登录
使用微信扫一扫登录