求函数y=2+arcsin(3+x)的反函数.
查看答案
相关试题
换一换


求函数y=2+arcsin(3+x)的反函数.
答案
函数y=f(x)存在反函数,若f(2)=-3,则函数y=f-1(x)的图像经过点( )
A.(-3,2) B.(1,3) C.(-2,2) D.(-3,3)
答案
函数y=3x-1的反函数是()。
答案
函数y=1+log2x(x>0)的反函数为()。
A.y=21-x(x∈R) B.y=2x-1(x∈R) C. 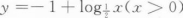 D.
D. 
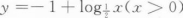 D.
D. 
答案
函数y=log3(x+1)的反函数为()。
A.y=3x-1 B.y=3x+1 C.y=3x-1 D.y=3x+1
答案
函数y=(x-1)2-4,(x≥1)的反函数为
A.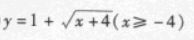 B.
B.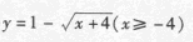 C.
C.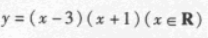 D.
D.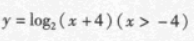
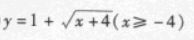 B.
B.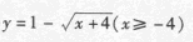 C.
C.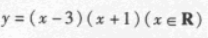 D.
D.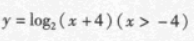
答案
函数y=arcsin(x-3)的自然定义域是()。
答案
函数y=ln(x+1)的反函数是()
A. B.
B.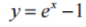 C.
C. D.x=ey-1
D.x=ey-1
 B.
B.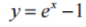 C.
C. D.x=ey-1
D.x=ey-1 答案
函数y=log5(x>0)的反函数是()
A.y=x5(x∈R) B.y=1/5x(x∈R) C.y=5x(x∈R) D.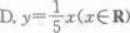
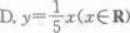
答案
函数y=log5x(x>0)的反函数是()。
A.y=x5(x∈R) B.y=1/5x(x∈R) C.y=5x(x∈R) D.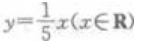
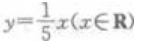
答案
热门试题
函数y=−x2(x≥0)y=−x2(x≥0)的反函数的定义域是( )。单项选择题选项:
求函数y=x3-3x2-9x+1的极值.
求函数(x,y)=x2+y2在条件2x+3y=1下的极值.
求函数(x,y)=x3+y3在条件x2+2y2=1下的最值.
函数z=arcsin(x2-2y)+ln(y-1)的定义域为()
已知函数f(x)=lg(x+1)。 (1)若0f(1-2x)-f(x)1,求x的取值范围; (2)若g(x)是以2为周期的偶函数,且当0≤x≤1时,有g(x)=f(x),求函数Y=g(x)(x∈[1,2])的反函数。
已知函数f(x)=lg(x+1)。 (1)若0<f(1-2x)-f(x)<1,求x的取值范围; (2)若g(x)9;g 2为周期的偶函数,且当0≤x≤1时,有g(x)=f(x),求函数y-=g(x)x∈[1,2])的反函数。
设函数y=x3+sinx+3,求y".
设y=(x3+4)/x2。 (1)求函数y的单调区间及极值; (2)求函数图像的凹凸区间及拐点; (3)求函数图像的渐近线; (4)作出函数的图形。
设函数f(x)=x3+2的反函数为g(x),则g(29)=()
设函数y=cos2x,求 y″=()
设函数y=cos2x,求 y″=()
已知函数y(x)由方程x^3+y^3-3x+3y-2=0确定,求y(x)的极值.
设函数y=y(x)由方程x2+y3-sinx+3y=0所确定,求函数y=y(x)在x=0处的法线方程。
若函数y=2x-1+3的反函数的图像经过点P,则点P的坐标是()。
求函数(x,y)=4(x-y)-x2-y2的极值.
设单调函数y=y(x)二次可导,且满足微分方程d2y/dx2+(dy/dx)3=0,则其反函数x=x(y)满足方程d2x/dy2=1。
设f(x)存在反函数,则其反函数
设函数y=sin(2x—1),求y".
若函数f(x)=log2(5x+1),则其反函数y=f-1(x)的图像过点( )



 使用微信扫一扫登录
使用微信扫一扫登录