对任意两个任意事件A,B,等式()成立。
A. P(A
B. =PA.PB.B.B.P(A+B.=P+PB.
C. P(A|B.=P(PB.≠0)
D. P(AB.=PP(B|A.(PA.≠0)
查看答案
相关试题
换一换


对任意两个任意事件A,B,等式()成立。
A.P(A B.=PA.PB.B.B.P(A+B.=P+PB. C.P(A|B.=P(PB.≠0) D.P(AB.=PP(B|A.(PA.≠0)
答案
对任意两事件A与B,等式()成立。
A.P(AB)=P(A)P(B) B.P(A∪B) =P(A)+P(B) C.P(A|B)=P(A)(P(B)≠0) D.P(AB)=P(A)P(B|A)(P(A)≠0)
答案
设A、B是任意两个事件,A?B,P(B)>0,则下列不等式中成立的是( )。
A.P(A)<P(A|B) B.P(A)≤P(A|B) C.P(A)>P(A|B) D.P(A)≥P(A|B)
答案
对满足a>b的任意两个非零实数,下列不等式成立的是()
A.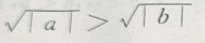 B.
B.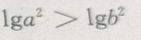 C.
C. D.
D.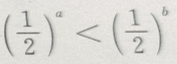
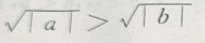 B.
B.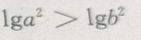 C.
C. D.
D.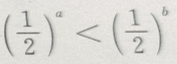
答案
对满足a>b的任意两个非零实数,下列不等式成立的是()。
A.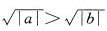 B.
B. C.
C.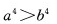 D.
D.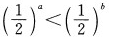
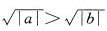 B.
B. C.
C.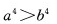 D.
D.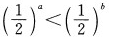
答案
若A 、B是两个任意事件,且P(AB)=0,则 ( )
答案
任意事件A和B,下列等式成立的是()。
A.P(A B.=PA.PB.B.B.P(AB.=PP(B/A. C.P+PB.=1 D.P(A+B.=P+PB.
答案
对于任意两个事件A和B( )。
A.若AB≠∅,则A与B一定独立 B.若AB≠∅,则A与B有可能独立 C.若AB=∅,则A与B一定独立 D.若AB=∅,则A与B一定不独立
答案
若A,B为任意两个随机事件,则( )。
A.P(AB)≤P(A)P(B) B.P(AB)≥P(A)P(B) C.P(AB)≤[P(A)+P(B)]/2 D.P(AB)≥[P(A)+P(B)]/2
答案
A,B为满足AB=0的任意两个非零矩阵,则必有( )
A.A的列向量组线性相关,B的行向量组线性相关 B.A的列向量组线性相关,B的列向量组线性相关 C.A的行向量组线性相关,B的行向量组线性相关 D.A的行向量组线性相关,B的列向量组线性相关
答案
热门试题
对于任意两事件A和B,若P(AB)=0,则( )。
设A,B为满足AB=0的任意两个非零矩阵,则必有( )。
设A,B为满足AB=0的任意两个非零矩阵,则必有
设A,B为满足AB=0的任意两个非零矩阵,则必有()。
对于任意两个事件A,B,必有P(A-B)=P(A)-P()
若P(A)=1,则对任意事件B,有P(AB)=P()
对于任意两个随机事件A和B,有P(A-B)等于
任意两个正方形相似吗?任意两个矩形呢?证明你的结论。
设A、B是任意两个随机事件,则P((A(_)∪B)(A∪B)(A(_)∪B(_))(A∪B(_)))=____。
如果A、B是任意两个随机事件,那么下列运算正确的是:()
对于任意两个事件A和B,下面的选项中正确的是()
中国大学MOOC: 设A, B为满足 AB = O 的任意两个非零矩阵, 则必有( ).
对于任意两个随机事件A与B,其对立的充分条件为()
中国大学MOOC: 设A,B是任意两个随机事件,则P(A-B)=( )
任意两个最大项之和为____
任意两个质数相加都是偶数()
已知a,b为任意正实数,则下列等式中恒成立的是()。
已知a,b为任意正实数,则下列等式中恒成立的是()。
若对任意实数x∈R,不等式|x|≥ax恒成立,则实数a的取值范围是( ).
任意两个函数都能构成复合函数。



 使用微信扫一扫登录
使用微信扫一扫登录