已知a,b为任意正实数,则下列等式中恒成立的是()。
A. ab=ba
B. 2a+b=2a+2b
C. 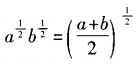 D. algb=blga
D. algb=blga
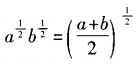
查看答案
相关试题
换一换


已知a,b为任意正实数,则下列等式中恒成立的是()。
A.ab=ba B.2a+b=2a+2b C.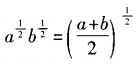 D.algb=blga
D.algb=blga
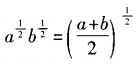 D.algb=blga
D.algb=blga 答案
已知a,b为任意正实数,则下列等式中恒成立的是()。
A.ab=ba B.2a+b=2a+2b C.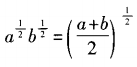 D.algb=blga
D.algb=blga
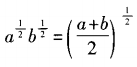 D.algb=blga
D.algb=blga 答案
已知a>b,若c是任意实数,则下列不等式中总是成立的是()
A.a+c<b+c B.a-c>b-c C.ac<bc D.ac>bc
答案
设a,b,c均为不等于1的正实数,则下列等式中恒成立的是()
A.logab·logcb=logca B.logab+logac=loga(bc) C.logabc=(logab)c D.loga(b+c)=logab+logac
答案
若对任意实数x∈R,不等式|x|≥ax恒成立,则实数a的取值范围是( ).
A.a<-1 B.|a|≤1 C.|a|<1 D.a≥1
答案
已知a>b,则下列等式恒成立的是()。
A.a²>b² B.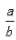 >1 C.
>1 C.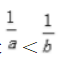 D.5a>5b
D.5a>5b
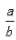 >1 C.
>1 C.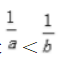 D.5a>5b
D.5a>5b 答案
不等式∣x+3∣-∣x-1∣≤a2-3a对任意实数x恒成立,则实数a的取值范围为
A.(-∞,-1]U[4,+∞) B.(一∞,一2]U[5,+∞) C.[1,2] D.(一∞,1]U[2,+∞) E.以上选项均不正确
答案
对满足a>b的任意两个非零实数,下列不等式成立的是()。
A.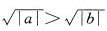 B.
B. C.
C.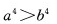 D.
D.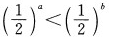
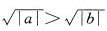 B.
B. C.
C.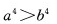 D.
D.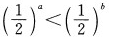
答案
对满足a>b的任意两个非零实数,下列不等式成立的是()
A.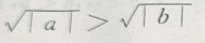 B.
B.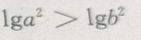 C.
C. D.
D.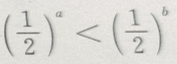
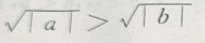 B.
B.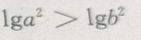 C.
C. D.
D.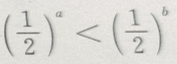
答案
若x∈[0,+∞),则下列不等式恒成立的是( )
A.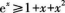 B.
B.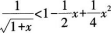 C.
C.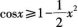 D.
D.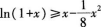
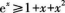 B.
B.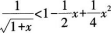 C.
C.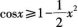 D.
D.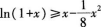
答案
热门试题
已知f(x)为偶函数,且y=f(x)的图像经过点(2,-5),则下列等式恒成立的是()
设A,B是n阶方阵,且AB=O.则下列等式成立的是().
设A,B是n阶方阵,且AB=0.则下列等式成立的是( ).
下列关系式中,对任意实数A<B<0都成立的是( )
下列关系式中,对任意实数A<B<0都成立的是()。
任意事件A和B,下列等式成立的是()。
设A、B是任意两个事件,A?B,P(B)>0,则下列不等式中成立的是( )。
若a>b,c>d>0,则下面的不等式恒成立的是( )
已知a,b,c是不完全相等的任意实数,若x=a2-bc,y=b2-ac,z=c2-ab,则x,y,x
对任意的实数k,直线y-2=k(χ+1)恒过定点M,则M的坐标是( )。
已知a>b,下列不等式成立的是
设函数f(x),g(x)在[a,b]上均可导(a<b),且恒正,若f′(x)g(x)+f(x)g′(x)>0,则当x∈(a,b)时,下列不等式中成立的是( )。
已知:x<a<0,则一定成立的不等式是()
对于任意实数x,恒有sinx≤X成立()
对任意的实数k,直线y-2=k(x+1)恒过定点M,则M的坐标是()。
对任意的实数k,直线y-2=k(x+1)恒过定点M,则M的坐标是( )。
对任意实数a、b、c定义运算a*b*c=ab-bc+ca,若1*x*2=2,则x=( )
x(t)δ(t) = x(0),等式恒成立()
对任意两个任意事件A,B,等式()成立。
已知a,b为实数.则a≥2或b≥2.(1)a+b≥4;(2)ab≥4.



 使用微信扫一扫登录
使用微信扫一扫登录