相关试题
换一换


设方程y''—2y'—3y=f(x)有特解y*,则它的通解为()
A. B.
B. C.
C.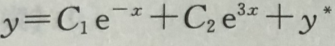 D.
D.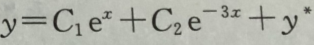
 B.
B. C.
C.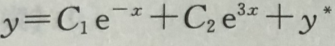 D.
D.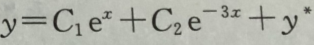
答案
设方程y”-2y'-3y=f(x)有特解y*,则它的通解为()
A.y=C1e-x+C2e3x+y* B.y=C1e-x+C2e3x C.y=C1xe-x-+C2e3x+y D.y=C1ex+C2e-3x+y*
答案
设y*是一阶线性非齐次微分方程的一个特解,y是其所对应的齐次方程的通解,则y=y+y²为一阶线性微分方程的通解()
答案
函数y1(x)、y2(x)是微分方程y′+p(x)y=0的两个不同特解,则该方程的通解为( )。
A.y=c1y1+c2y2 B.y=y1+cy2 C.y=y1+c(y1+y2) D.y=c(y1-y2)
答案
方程y″-3y′+2y=excos2x的特解形式y*=( )。
A.excos2x B.xex(Acos2x+Bsin2x) C.ex(Acos2x+Bsin2x) D.x2ex(Acos2x+Bsin2x)
答案
设y1=x,y2=x+e2x,y3=x(1+e2x)是二阶常系数线性非齐次方程的特解,求该方程及其通解。
答案
设y1=x,y2=ex,y3=e-x是y”+py'+qy=f(x)(其中p、q都是常数)的三个特解,则该方程的通解为().
答案
求微分方程y”-3y'+2y=2的通解。
答案
设二阶线性微分方程y″+P(x)y′+Q(x)y=f(x)的三个特解是y1=x,y2=ex,y3=e2x,试求此方程满足条件y(0)=1,y′(0)=3的特解。
答案
设y1=3+x2,y2=3+x2+e-x是某二阶线性非齐次微分方程的两个特解,且相应的齐次方程有一个解为y3=x,则该方程的通解为____。
答案
热门试题
已知微分方程y"+p(x)y = q(x)[q(x)≠0]有两个不同的特解y1(x), y2(x),C为任意常数,则该微分方程的通解是:
已知微分方程y"+p(x)y=q(x)[q(x)≠0]有两个不同的特解:y1(x),y2(x),则该微分方程的通解是:(c为任意常数)
微分方程y'-2y=3的通解为=()。
已知方程xy″+y′=4x的一个特解为x2,又其对应的齐次方程有一特解lnx,则它的通解为( )。
方程y"y-(y’)
2=0的通解为()。
方程y"+2y’+y=0的通解为()。
(2012)已知微分方程y′+p+(x)y=q(x)[q(x)≠0]有两个不同的特解y1(x),y2(x),则该微分方程的通解是:(c为任意常数)()
已知齐次方程xy´´+y´=0有一个特解为lnx,则该方程的通解为( ).
求方程y”-2y'-3y=3x+1的一个特解.
微分方程y/=3x2 的通解为y=()
微分方程y/=3x2 的通解为y=()
微分方程y""-3y"+2+2y=xex的待定特解的形式是:
求微分方程y"-3y"+2y=2xe^x的通解.
微分方程y"-3y"+2y=xex的待定特解的形式是:
微分方程y'=2y的通解为y=()。
已知y1(x)与y2(x)是方程y″+P(x)y′+Q(x)y=0的两个线性无关的特解,Y1y′+Q(x)y=R1(x)和y″+P(x)y′+Q(x)y=R2(x)的特解。那么方程y″+P(x)y′+Q(x)y=R1(x)+R2(x)的通解应是()
已知y1(x)与y2(x)是方程y″ P(x)y′ Q(x)y=0的两个线性无关的特解,Y1(x)和Y2(x)分别是是方程y″ P(x)y′ Q(x)y=R1(x)和y″ P(x)y′ Q(x)y=R2(x)的特解。那么方程y″ P(x)y′ Q(x)y=R1(x) R2(x)的通解应是:()
3阶常系数线性齐次微分方程y?-2y″+y′-2y=0的通解y=
已知y1(X)与y2(x)是方程:y" + P(x)y"+Q(x)y = 0的两个线性无关的特解,y1(x)和y2(x)分别是方程y"+P(x)y"+Q(x)y=R1(x)和y"+p(x)+Q(x)y=R2(x)的特解。那么方程y"+p(x)y"+Q(x)y=R1(x)+R2(x)的通解应是:
(2013)微分方程y″-3y′+2y=xex的待定特解的形式是:()



 使用微信扫一扫登录
使用微信扫一扫登录