在平面内,若直线a⊥c,直线b⊥c,则a∥b;在空间中,若直线a⊥c,直线b⊥c,则直线a与直线b不一定平行。这说明()
A. 人们难以完全正确地反映客观事物
B. 人们对事物的认识具有反复性
C. 真理具有客观性
D. 任何真理都有自己适用的条件和范围
查看答案
相关试题
换一换


在平面内,若直线a⊥c,直线b⊥c,则a∥b;在空间中,若直线a⊥c,直线b⊥c,则直线a与直线b不一定平行。这说明()
A.人们难以完全正确地反映客观事物 B.人们对事物的认识具有反复性 C.真理具有客观性 D.任何真理都有自己适用的条件和范围
答案
中国大学MOOC: 若点C在直线AB上,则必有AC:CB=ac:cb。
答案
直线AC,B为AC中点,AB、BC测距中误差均为±2cm,则AC距离中误差为()
A.±2.0cm B.±2.8cm C.±4.0cm D.±8.0cm
答案
若直线 AB 与平面 P 垂直,且平面 P 为正垂面,则直线 AB 是( )。
A.正平线 B.水平线 C.侧平线 D.一般位置直线
答案
已知直线 AB 和平面 P 的标高投影,判断直线 AB 与平面 P 的位置关系,若直线 AB 上一点的标高与平面 P 上同一点的标高相同,则直线 AB 与平面 P( )。
A.平行 B.相交 C.垂直 D.无法确定11
答案
在平面内,若直线a垂直于c,直线b垂直于c,则直线a平行直线b;在空间,若直线a垂直于c,直线b垂直于c,则直线a与直线b不一定平行。从哲学上看,这说明()。
答案
若平面α//平面β,直线l//α,则()
A.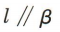 B.
B.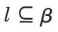 C.
C.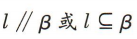 D.
D.
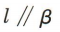 B.
B.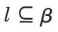 C.
C.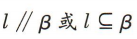 D.
D.
答案
已知直线l,m和平面α,若直线l在平面α内,则下列结论正确的是()
A.若m//α,则m//l B.若m⊥l,则m⊥α C.若m//l,则m//α D.若m⊥α,则m⊥l
答案
AB直线,C为AB中点,分别4次量取AC、CB距离,若单次量距中误差均为±4cm,则AB距离的中误差为()
A.±2cm B.±2.8cm C.±4cm D.±8cm
答案
若实数a>b>c,则ac>bc。()
答案
热门试题
若点A在直线a上,直线a在平面α内,点B在α内,则下列表述正确的是()
已知直线AB及一点P,若过点P作一条直线与AB平行,则这样的直线()
若平面α||平面β,直线a⊂α,直线b⊂β那么直线a、b的位置关系是( )
已知直线a,b,平面a,β.若a//a,b//a,则直线a,b的位置关系是().
若一直线过平面上一点且垂直于该平面上的另一直线,则此直线在该平面内
若直线a⊥平面α,则过直线a有且只有一个平面与已知平面α垂直。()
分别和两条异面直线AB、CD同时相交的两条直线AC、BD( )
分别和两条异面直线AB、CD同时相交的两条直线AC、BD()。
若直线l与平面M平行,则在平面M内与l垂直的直线()
假设空间中的直线AB和CD平行,则下列说法正确的是()
AB+AC+BC=AB+ AC 。( )
若a>b,ac<bc,则一定有( )。
已知直线 AB 和直线 CD 的标高投影,判断两直线是否平行,若两直线的坡度相同且方向一致,则两直线( )。
如果ac<0,bc<0,那么直线ax+by+c=0不通过()
若一个平面内的两条相交直线分别平行于另一平面内的相交两直线,则连两平面()
若空间两直线的三个投影均相交,则空间两直线必相交
在空间中,过直线外一点与该直线平行的平面( )
若直线l是平面α的一条斜线,则在平面α内与l垂直的直线( ).
若直线的方向向量和平面的法向量的数量积为零,则直线与平面.
若直线a与平面α有公共点,则称a∈α()



 使用微信扫一扫登录
使用微信扫一扫登录