设L为直线,则曲线积分______/ananas/latex/p/1966661/ananas/latex/p/1966667
查看答案
相关试题
换一换


设L为直线,则曲线积分______/ananas/latex/p/1966661/ananas/latex/p/1966667
答案
设L为从点A(0,-2)到点B(2,0)的有向直线段,则对坐标的曲线积分ydy等于()
A.1 B.-1 C.3 D.-3
答案
设曲线y=e2x+x-1在点(0,0)处与直线l相切,则直线l的斜率为()
A.不存在 B.1 C.3 D.-2
答案
设方程y´´-4y´+3y=0的某一积分曲线,它在点(0,2)处与直线x-y+2=0相切,则该积分曲线的方程是( ).
A.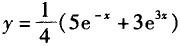 B.
B.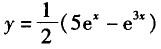 C.
C.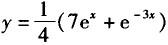 D.
D.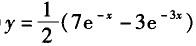
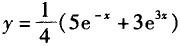 B.
B.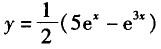 C.
C.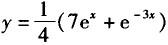 D.
D.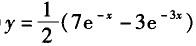
答案
设曲线y=1/x与直线y=x及x=2所围图形的面积为A,则计算A的积分表达式为( ).
A.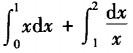 B.
B.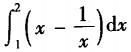 C.
C.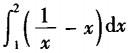 D.
D.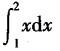
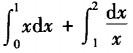 B.
B.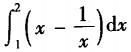 C.
C.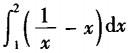 D.
D.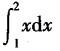
答案
设C为圆周x2+y2=ax(a>0),则曲线积分的值是().
A.a2 B.2a2 C.3a2 D.4a2
答案
设L是抛物线上从点A(1,1)到点O(0,0)的有向弧线,则对坐标的曲线积分等于()
A.0 B.1 C.-1 D.2
答案
设L为正向圆周x2+y2=2在第一象限中的部分,则曲线积分∫Lxdy-2ydx的值为____。
答案
设L是抛物线y=上从点A (1, 1)到点O (0, 0)的有向弧线,则对坐标的曲线积分等于()
A.0 B.1 C.-1 D.2
答案
设L为正向圆周x^2+y^2=2在第一象限中的部分,则曲线积分∫Lxdy-2ydx的值为( )。
A.3π/2 B.2π/3 C.3π/4 D.4π/3
答案
热门试题
()不仅可留设直线孔道,也能留设曲线孔道
设L为抛物线y=x2上从0(0,0)到P(1,1)的一段弧,则曲线积分的值是().
设竖曲线半径为R,长度为L,则竖曲线中点处的纵距y为()
设直线方程为则该直线()。
设直线方程为,则该直线()
设直线L为,平面π为4x-2y+z-2=0,则直线和平面的关系是()
设曲线积分∫L[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。
积分环节的对数幅频特性曲线是一条直线,直线的斜率为( )dB/dec。
设直线L为 平面π为4x-2y+z-2=0,则直线和平面的关系是( )。
设圆周曲线L:值等于()
设曲线积分∮L2[xφ(y)+ψ(y)]dx+[x2ψ(y)+2xy2-2xφ(y)]dy=0,其中L为任意一条平面曲线。求: (1)可微函数φ(y)、ψ(y)。已知φ(0)=-2,ψ(0)=1。 (2)求沿L从原点(0,0)到点M(π,π/2)的曲线积分。
直线AB的正方位角αAB为196°,则其反方位φBA为()
已知曲线L的方程为y=1-|x|(x∈[-1,1]),起点是(-1,0),终点为(1,0),则曲线积分________.
设竖曲线的半径为R,竖曲线长度为L,坡度角为ω,则三者的关系为()
从微积分的角度来讲,解决几何问题的方法是以直线代替曲线()
设曲线L的方程为y=x2/4-lnx/2(1≤x≤e)。(Ⅰ)求L的弧长;(Ⅱ)设D是由曲线L,直线x=1,x=e及x轴所围平面图形,求D的形心的横坐标。
已知平面α,两条直线l1,l2。设甲:l1⊥α且l2⊥α;乙:l1//l2,则()。
路线上平面测设线(平曲线)一般由直线、圆曲线、缓和曲线组成。
正线与联络线上曲线半径小于时,直线与圆曲线间要设缓和曲线()
设a∈R,则a=1是直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行的( )



 使用微信扫一扫登录
使用微信扫一扫登录