若f(x)与g(x)在x→x0时都是无穷小且f(x)≠0,则下列极限等式正确的是()
A. 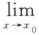 [f(x)+g(x)]=∞
B.
[f(x)+g(x)]=∞
B. 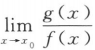 =0
C.
=0
C. 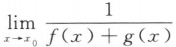 =0
D.
=0
D. 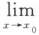 bf(x)=0(b为非零常教)
bf(x)=0(b为非零常教)
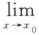 [f(x)+g(x)]=∞
[f(x)+g(x)]=∞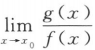 =0
=0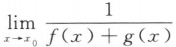 =0
=0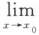 bf(x)=0(b为非零常教)
bf(x)=0(b为非零常教)查看答案
相关试题
换一换


若f(x)与g(x)在x→x0时都是无穷小且f(x)≠0,则下列极限等式正确的是()
A.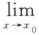 [f(x)+g(x)]=∞ B.
[f(x)+g(x)]=∞ B.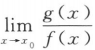 =0 C.
=0 C.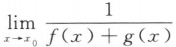 =0 D.
=0 D.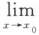 bf(x)=0(b为非零常教)
bf(x)=0(b为非零常教)
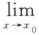 [f(x)+g(x)]=∞ B.
[f(x)+g(x)]=∞ B.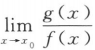 =0 C.
=0 C.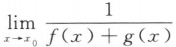 =0 D.
=0 D.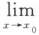 bf(x)=0(b为非零常教)
bf(x)=0(b为非零常教) 答案
当x→0时,若x-tanx与xk是同阶无穷小,则k=( )。
A.1 B.2 C.3 D.4
答案
以下说法正确的是: 0是无穷小|无穷小就是0|无穷小时最小的常数|是无穷小/ananas/latex/p/22026
答案
若x→0时,[(1–ax2)1/4-1]与xsinx是等价无穷小,则a=____。
答案
当x→0时,若x-tan x与x^k是同阶无穷小,则k=
A.A1 B.2 C.3 D.4
答案
已知x→0时,f(x)是无穷小量,且f(x)≠0,则下列函数在x→0时为无穷大量的是()
A.2f(x) B.f(x)+a(a为常数) C.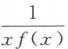 D.f(x2)
D.f(x2)
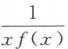 D.f(x2)
D.f(x2) 答案
当x→0时,下列哪一个无穷小是x的三阶无穷小?()
A.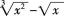 B.
B.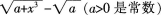 C.
C.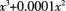 D.
D.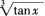
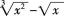 B.
B.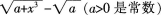 C.
C.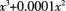 D.
D.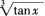
答案
当x→0时,下列函数与x是等价无穷小的是()。
A. B. C.e -x-1 D.
答案
公式C=kαFX0(e-kt-e-kαt)/V(kα-k)表示
A.单室单剂量血管外给药C-t关系式 B.单室单剂量静脉滴注给药C-t关系式 C.单室单剂量静脉注射给药C-t关系式 D.单室多剂量静脉注射给药C-t关系式 E.多剂量函数
答案
当x→0时,下列四个无穷小中,比其他三个更高阶的无穷小是()
A.x2 B.1-cosxr C. -1 D.
-1 D.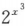 -1
-1
 -1 D.
-1 D.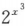 -1
-1 答案
热门试题
当x→0时,下列变量中为无穷小的是()
当x→x0时,与x-x0。是等价无穷小的为()。
设α、β是同一过程中的两个无穷小,且α不等于0,如果lim β/α=0,则___()
当x→x0时,与x-x0叫。是等价无穷小的为()。
当x→x0时,与x-x0叫。是等价无穷小的为()。
当x→0+时,与x是等价无穷小的是().
0不可以作为无穷小.
当x→0时,无穷小1-cosx等价于()
设x→0时,e^tanx-e^x与x^n是同阶无穷小,则n为( )。
设x→0时,e^tanx-e^x与x^n是同阶无穷小,则n为()
当x→0时,α(x)=sin2x和β(x)=x3+3x都是无穷小,则α(x)是β(x)的().
已知当x→0时,sinx-,是atanx3的等价无穷小,则a=().
当x→0时,无穷小x-sinx是x的()
已知当x→0时,函数f(x)=3sinx-sin3x与cxk是等价无穷小,则( )。
设函数f(x,y)在点(0,0)附近有定义,且fx′(0,0)=3,fy′(0,0)=1,则( )。
当x→0时,若sin2x与xk是等价无穷小量,则k=()()。
当x趋于0时,若sin2x与xk是等价无穷小量,则k=().
y=fx在点x0连续,则y=fx在点x0必定可导()
当x→0时,下列为无穷小量的是().
已知当x→0时,(1+ax2)1/3-1与cosx-1是等价无穷小,则常数a=____。



 使用微信扫一扫登录
使用微信扫一扫登录