偶函数y= f(x)在(-∞,1)上是增函数,则f(x)在(1,+∞)上是()
A. 增函数
B. 减函数
C. 先增后减
D. 先减后增
查看答案
相关试题
换一换


偶函数y= f(x)在(-∞,1)上是增函数,则f(x)在(1,+∞)上是()
A.增函数 B.减函数 C.先增后减 D.先减后增
答案
下列函数中既是偶函数又是(-∞,0)上的增函数的是()
A.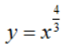 B.
B.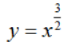 C.
C.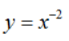 D.
D.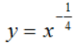
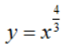 B.
B.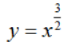 C.
C.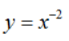 D.
D.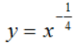
答案
已知偶函数f(x)在[-1,0]上是增函数,且最大值为5,那么f(x)在[0,1]上是( ).
A.增函数,最小值为5 B.增函数,最大值为5 C.减函数,最小值为5 D.减函数,最大值为5
答案
已知定义在实数集R上的偶函数?(x)在区间[0,+∞)上为单调增函数,若?(1)
答案
已知偶函数y=ƒ(x)在区间[a,b](0
A.增函数 B.减函数 C.不是单调函数 D.常数
答案
已知偶函数y=f(x),在区间[a,b](0
A.增函数 B.减函数 C.不是单调函数 D.常数
答案
已知偶函数y=f(x)在区间[a,b](0
A.增函数 B.减函数 C.不是单调函数 D.常数
答案
若奇函数f(x)在[1,3]上是增函数,且最小值是1,则f(x)在[-3,-1]上是()
A.增函数,最小值是-1 B.增函数,最大值是-1 C.减函数,最小值是-1 D.减函数,最大值是-1
答案
已知函数f(x)是奇函数,且在区间[1,2]上单调递减,则f(x)在区间[-2,-1]上是单调递增函数。()
答案
下列函数中,在区间(0,1)上是增函数的是()
A.y=|x+1| B.y=2-x C.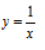 D.y=x2-x+1
D.y=x2-x+1
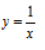 D.y=x2-x+1
D.y=x2-x+1 答案
热门试题
若函数f(x)=(m-1)x+1在R上是增函数,则f(m)与f(1)的大小关系是()
指数函数f(x)=(a-1)x在R上是增函数,则a的取值范围是().
设f(x)是[-2,2]上的偶函数,且f'(-1)=3,则f'(1)=()
设f(x)是[-2,2]上的偶函数,且f′(-1)=3,则f′(1).
下列函数中,既是偶函数,又是区间(0,+∞) 内的增函数是( ).
已知f(x)在R上是偶函数,若f(-2)=1,则f(2)=( )。
若函数y=(a+1)x+b是增函数,则()
若偶函数f(x)在[1,5]上是单调递增,且最小值是1,则f(x)在[-5,-1]上()
下列函数中,在区间(0,1)(0,1)上是增函数的是( )。单项选择题选项:
已知二次函数y=x2+ax+1在区间[1,+∞)上为递增函数,则实数a的取值范围是( )
已知函数f(x)在[3-2a,a]上是偶函数,则实数a=()
下列函数是R上的增函数的是( )。
若f(x)为偶函数,且在(0,+∞)为增函数,则下列不等式成立的是()。
下列函数中,在(0,+∞)上是增函数的是()
设f(x)是定义在[-a,a]上的任意函数,则下列答案中哪个函数不是偶函数?()
下列函数在R上既是奇函数又是增函数的是( )。
下列函数在R上既是奇函数又是增函数的是( )。
下列函数中,在R上为增函数的是()
下列函数中,在区间(0,+∞)上是增函数的是()
如果偶函数f(x)在区间(0,1).上是减函数,且最大值为3,那么f(x)在区间(-1,0)上是()



 使用微信扫一扫登录
使用微信扫一扫登录