已知x2-5∣x+1∣+2x-5=0,则x的所有取值的和为
A. 2
B. -2
C. 0
D. 1
E. -1
查看答案
相关试题
换一换


已知x2-5∣x+1∣+2x-5=0,则x的所有取值的和为
A.2 B.-2 C.0 D.1 E.-1
答案
已知集合A={x|x<2a-1},B={x|x≥1},且A∪B=R,则实数a的取值范围是()
答案
已知集合A={x|log2x
A.(-∞,2] B.[1,+∞) C.(0,2] D.[2,+∞)
答案
已知(x)在区间(-∞,+∞)内为单调减函数,且(x)>(1),则x的取值范围是().
A.(-∞,-l) B.(-∞,1) C.(1,+∞) D.(-∞,+∞)
答案
已知x=12,则执行x='abc'后,变量x的值是()
A.12 B.'abc' C.abc D.无法确定
答案
已知x的值大于3,则x的取值范围可用区间表示为( )。
A.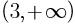 B.
B.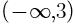 C.
C.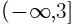 D.
D.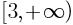
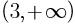 B.
B.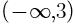 C.
C.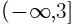 D.
D.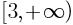
答案
已知函数f(x)=x²-2x+3在[a,3]上的取值范围为[2,6],则实数a的取值范围是()
A.(-0,1] B.[-2,-1] C.[-1,1] D.[-2,1]
答案
已知集合A={x|x2-3x-4>0},集合B={x|m+1≤x≤4m},若B?A,则实数m的取值范围为()。
A.(-∞,3) B.(-(1/4),3) C.(-∞,-(1/4))∪(3,+∞) D.(-∞,1/3)∪(3,+∞)
答案
离散型随机变量X,X所有取值为0,1,2,且P(X=0)=0.5,P(X=1)=0.25,P(X=2)=0.25,则P(X
A.0 B.0 C.0 D.1
答案
已知函数f(x)=x2-6x+8,x∈[1,a],且函数f(x)的最小值为f(a),则实数a的取值范围是()
A.(1,2) B.(1,3] C.(1,4] D.(1,5]
答案
热门试题
已知函数f(x)在区间(-∞,+∞)单调增加,则使f(x)>f(2)成立的x的取值范围是()。
设A={x∣x2-2x-3≤0},B={x∣x≤a},若A∩B=A,则a的取值范围是( )。
已知函数f(x)在区间(-∞,+∞)上单调增加,则使f(x)>f(2)成立的x的取值范围是().
若|x|<1,则 x 的取值范围是( )。
若|x|>3 ,则x的取值范围是( )。
若|x|>3,则x的取值范围是( )。
若|x|>3,则x的取值范围是( )。
若|x|<1,则x的取值范围是 ( )。
已知函数f(x)=|x-2|,g(x)=|2x+3|-|2x-1|.(1)画出y=f(x)和y=g(x)的图像.(2)若f(x+a)≥g(x),求a的取值范围
已知集合A={x│x>2},B={x│0<x<4},则A∪B=( )
已知x1,x2是方程x2-ax-1=0的两个实根,则x12x22=
若x满足x2-x-5大于∣1-2x∣,则x的取值范围为
已知X满足:P{X>x}=e–x对所有x>0成立,那么X的分布是:()
已知|x|-8=0,则x=()
已知|x|-3=0,则x=()
已知“int x=6;”,则执行语句“x+=x-=x*x”后x的值是
已知p:│x│=x,q:x²≥-x,则p是q的( )条件
已知集合A={x|-1
已知集合A={x|-1≤x<2},B={y|y≤m},若A∪B=B,则m的取值范围是()
已知函数f(x)=x(x∈R),则f(2)=()



 使用微信扫一扫登录
使用微信扫一扫登录