某校计划修建一座既是中心对称图形又是轴对称图形的花坛,征集到的设计方案有等边三角形,正五边形,平行四边形,正八边形四种图案,你认为符合条件的是( )
A. 等边三角形
B.
C. 正五边形
D.
E. 平行四边形
F.
G. 正八边形
查看答案
相关试题
换一换


下列图形既是轴对称图形,又是中心对称图形的是()。
A.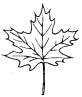 B.
B. C.
C. D.
D.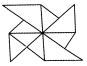
 B.
B. C.
C. D.
D.
答案
下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等边三角形 B.等腰梯形 C.正五边形 D.正六边形
答案
下列图形中,既是轴对称图形,又是中心对称图形的是()。
A.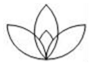 B.
B. C.
C.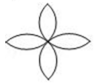 D.
D.
 B.
B. C.
C. D.
D.
答案
下列图形既是中心对称又是轴对称的是
答案
下列几何图形中,既是轴对称图形又是中心对称图形的是
A.等边三角形 B.矩形 C.平行四边形 D.等腰梯形
答案
下列四个图形中,既是中心对称图形,又是轴对称图形的是()
A.选项1 B.选项2 C.选项3 D.选项4
答案
下列所给的几个图形中,既是轴对称图形,又是中心对称图形的是()
A. B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
下列图形中,是轴对称图形但不是中心对称图形的是()
A. B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
在角、等边三角形、矩形和双曲线四个图形中,既是轴对称图形又是中心对称图形的有( )。
A.1个 B.2个 C.3个 D.4个
答案
某校计划修建一座既是中心对称图形又是轴对称图形的花坛,征集到的设计方案有等边三角形,正五边形,平行四边形,正八边形四种图案,你认为符合条件的是()
A.等边三角形 B.正五边形 C.平行四边形 D.正八边形
答案
热门试题
某校计划修建一座既是中心对称图形又是轴对称图形的花坛,征集到的设计方案有等边三角形,正五边形,平行四边形,正八边形四种图案,你认为符合条件的是( )
在角、等边三角形、矩形和双曲线四个图形中,既是轴对称又是中心对称的图形有()。
在角、等边三角形、矩形和双曲线四个图形中,既是轴对称又是中心对称的图形有()。
下列四个图案中,是中心对称图形,但不是轴对称图形的是()
等边三角形是轴对称图形,也是中心对称图形()
下列图形不是中心对称图形的是()。
下列图形不是中心对称图形的是( )。
可以把“平行图形的对称”——轴对称、n次中心对称、平移对称用到的运动氛围三类:反射、旋转、平移()
中心对称和中心对称图形的教学目的主要有①知道中心对称的概念,能说出中心对称的定义和关于中心对称的两个图形的性质。②会根据关于中心对称图形的性质定理2的逆定理来判定两个图形关于一点对称;会画与已知图形关于一点成中心对称的图形。此外,通过复习图形轴对称,并与中心对称比较,渗透类比的思想方法;用运动的观点观察和认识图形,渗透旋转变换的思想。 通过题干来完成下列教学设计。 (1)给出本课程的课题引入; (2)根据教学目标设计教学环节;给出两个实例以进行知识探究。
四个图形:相交直线、等腰三角形、平行四边形、正多边形,既是轴对称又是中心对称的有( )个。
谈谈你对内容标准中“认识并欣赏自然界和现实生活中的轴对称、中心对称图形,运用图形的轴对称、旋转、平移进行图案设计”要求的认识。
谈谈你对内容标准中“认识并欣赏自然界和现实生活中的轴对称、中心对称图形,运用图形的轴对称、旋转、平移进行图案设计”要求的认识。
下列图形中,不是中心对称图形的是()
圆是以什么为对称中心的中心对称图形?
“中心对称和中心对称图形”的教学目的主要有①知道中心对称的概念,能说出中心对 称的定义和关于中心对称的两个图形的性质。②会根据关于中心对称图形的性质定理2的逆 定理来判定两个图形关于一点对称;会画与已知图形关于一点成中心对称的图形。此外,通过复习图形轴对称,并与中心对称比较,渗透类比的思想方法;用运动的观点观察和认识图形,渗透旋转变换的思想。 通过题干来完成下列教学设计。 (1)给出本课程的课题引入; (2)根据教学目标设计教学环节;给出两个实例以进行知识探究。
什么是轴对称图形?下面两个图形是轴对称图形吗?
下列不是中心对称图形的是()
正多边形都是中心对称图形。()
轴对称图形一定有对称轴()
对称的形式有中心对称 、 轴对称,旋转对称 反转对称,移动对称等



 使用微信扫一扫登录
使用微信扫一扫登录