如图所示铰接四边形机构中,O1 A= O2 B =100mm,又O1O2= AB,杆O1A以等角速度ω= 2 rad/s绕O1 轴转动。杆AB上有一套筒C,此筒与杆CD相铰接。机构的各部件都_
查看答案
相关试题
换一换


如图所示铰接四边形机构中,O1 A= O2 B =100mm,又O1O2= AB,杆O1A以等角速度ω= 2 rad/s绕O1 轴转动。杆AB上有一套筒C,此筒与杆CD相铰接。机构的各部件都_
答案
中国大学MOOC: 如图所示铰接四边形机构中,O1 A= O2 B =100mm,又O1O2= AB,杆O1A以等角速度ω= 2 rad/s绕O1 轴转动。杆AB上有一套筒C,此筒与杆CD相铰接。机构的各部件都在同一铅直面内。求当? = 60°时,杆CD 的速度和加速度。 【图片】
答案
在复平面内,点A 和C 对应的复数分别为4-2i和-2+4i,若四边形O4BC为平行四边形,o(为坐原点),则点B对应的复数为 ()
A.1+i B.1-i C.2-2i D.2+2i
答案
已知四边形ABCD的对角线相交于O,给出下列4个条件:①AB∥CD;②AD∥BC;③AB=CD;④∠BAD=∠DCB.从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有()
A.6组 B.5组 C.4组 D.3组
答案
已知四边形ABCD的对角线相交于o,给出下列5个条件①AB//CD②ADllBC③AB=CD④∠BAD=∠DCB,从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有()
A.6组 B.5组 C.4组 D.3组
答案
设甲:四边形ABCD是平行四边形,乙:四边形ABCD是正方形,则()。
A.甲是乙的充分条件,但不是乙的必要条件 B.甲是乙的必要条件,但不是乙的充分条件 C.甲是乙的充分必要条件 D.甲不是乙的充分条件,也不是乙的必要条件
答案
如图,几个四边形是同一个四边形缩小(保持形状不变)而得到的。1、在图中标出各个四边形的外角;2、在缩小的过程中四边形的对应的各个外角的大小是否发生了变化?3、如果保持四边形的形状不变,将四边形不断缩小下去,你能想象一下最终的形状吗?你能借助上面的变化过程说明四边形的外角和吗?4、你能类似地说明五边形、六边形……一般多边形的外角和吗?
答案
顺次连接四边形ABCD的各边中点所得的四边形是()
A.矩形 B.菱形 C.平行四边形 D.正方形
答案
日常生活中,我们随处可见四边形的物体,那么有两组对边平行的四边形,这样的四边形邻角()
答案
下列条件中,能判定四边形ABCD为平行四边形的是()
A.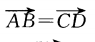 B.
B. C.
C. D.
D.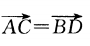
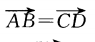 B.
B. C.
C. D.
D.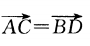
答案
热门试题
平行四边形机构是()机构。
“四边形的四条边相等”是“四边形是正方形”的()
四边形属于()形。
如图,平行四边形ABCD的对角线AC、BD交于点O,AD=8,BD=12,AC=6,则△OBC的周长为()
如果一个四边形是中心对称图形,那么这个四边形一定是平行四边形吗?为什么?
设命题甲:四边形为菱形,命题乙:四边形为平行四边形,则甲是乙的必要不充分条件。()
平行四边形机构为双曲柄机构。
已知平行四边形ABCD的三个顶点为A(-3,0),B(2,-2),C(5,2),且对角线交点为O,求顶点D的坐标及点O的坐标.
平面α外一点P到平面α内的四边形的四条边的距离都相等,且P在α内的射影在四边形内部,则四边形是()
小学生学习了四边形以后,再学习平行四边形。这种学习属于()。
(名词解析)四边形(Quadrilateral)
设M={平行四边形},N={四边形},P={矩形},则这些集合之间的关系为()
三角形和四边形是最基本的框架,四边形框架的稳定性最好()
三角形和四边形是最基本的框架,四边形框架的稳定性最好()
学生已经有“四边形”的概念,现在要学习“平行四边形”,这是一种()。
用向量的方法证明:对角线互相平分的四边形ABCD是平行四边形.
四级“四边形分类”中主要介绍了()
小学生在学习了四边形之后在学习平行四边形,这种学习属于( )
请以四边形为属概念,选择不同的概念种差,给出平行四边形的几组定义。
《义务教育教学课程标准》关于平行四边形的性质的教学要求是:探索并证明平行四边形的性质定理——平行四边形的对边以及对角相等,请基于该要求,完成下列教学设计任务:(1)设计平行四边形性质的教学目标;(2)设计两种让学生发现平行四边形性质的教学流程;(3)设计平行四边形性质证明的教学流程,使学生领悟证明过程中的教学思想方法



 使用微信扫一扫登录
使用微信扫一扫登录