掷均匀硬币一次,事件“出现正面或反面”的概率为________。
A. 1
B. 5
C. 4
D. 1
查看答案
相关试题
换一换


掷均匀硬币一次,事件“出现正面或反面”的概率为( )。
A.1 B.4 C.5 D.1
答案
掷均匀硬币一次,事件“出现正面或反面”的概率为________。
A.1 B.5 C.4 D.1
答案
将一枚硬币独立地掷两次,以A1、A2、A3、A4依次表示事件“第一次出现正面”,“第二次出现正面”、“正、反面各出现一次”,“正面出现两次”,则事件( )。
A.1,A2,A3相互独立 B.2,A3,A4相互独立 C.1,A2,A3两两独立 D.2,A3,A4两两独立
答案
掷五个硬币,出现五个正面或三个反面的概率是
答案
扔一枚质地均匀的硬币,我们知道出现正面或反面的概率都是0.5,这属于概率应用方法中的()。
A.古典概率方法 B.统计概率方法 C.主观概率方法 D.样本概率方法
答案
假设扔一枚质地均匀的硬币,我们知道出现正面或反面的概率都是0.5,这属于概率应用方法中的()。
A.古典概率方法 B.先验概率方法 C.主观概率方法 D.样本概率方法 E.统计概率方法
答案
一枚硬币投掷三次,或三枚硬币各掷一次,出现两次或两次以上正面的概率是1/2。()
A.错误 B.正确
答案
一枚伍分硬币连抛3次,只有一次出现正面的概率为()
A.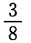 B.
B.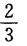 C.
C.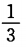 D.
D.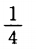
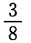 B.
B.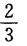 C.
C.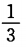 D.
D.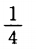
答案
投掷两次硬币,出现“正面,反面”的概率是()。
A.0.50 B.0.33 C.0.25 D.0.125
答案
掷一枚均匀硬币直到出现3次正面才停止. (1)问正好在第6次停止的概率; (2)问正好在第6次停止的情况下,第5次也是出现正面的概率.
答案
热门试题
将一枚均匀的硬币抛两次,事件分别表示“第一次出现正面”,“两次出现同一面”,“至少有一次出现正面”。则下述中不正确的是()。
一枚硬币掷3次,出现两次或两次以上正面的概率是()
独立地抛掷一枚质量均匀硬币,已知连续出现了10 次反面,问下一次抛掷时出现的是正面的概率是:()
某同学掷一枚硬币,结果是一连9次都掷出正面朝上,请问他第10次掷出硬币时出现正面朝上的概率为()
某同学掷一枚硬币,结果是一连9次都掷出正面朝上,请问他第10次掷出硬币时出现正面朝上的概率为()
同时抛掷三枚均匀的硬币,正面与反面都出现的概率为( )。
一枚硬币掷三次,出现两次正面在上的概率是()
将一枚质地均匀的硬币连续投掷2次,则2次都出现正面向上的概率为()
随机掷一枚均匀的硬币两次,两次正面都朝上的概率是()
一个硬币连续拋掷三次,出现三次正面的概率是()
某硬币正面朝上的概率为0.3,投掷4次才出现正面朝上的概率为()
把一枚质地均匀的硬币连续抛三次,以X表示在三次中出现正面的次数,Y表示在三次中出现正面的次数与出现反面的次数的差的绝对值,则{X=2,Y=1}的概率为()
抛一枚硬币,反复抛4次,恰有3次出现正面的概率为()
同时掷3枚均匀硬币,则恰2枚正面朝上的概率为()
一个硬币掷10次,其中5次正面向上的概率是0.5。
一个硬币掷10次,其中5次正面向上的概率是0.5()
一个硬币掷10次,其中5次正面向上的概率是0()
一个硬币掷对0次,其中5次正面向上的概率是0.5()
同时掷3枚均匀的硬币,则恰有2枚正面向上的概率为
同时掷3枚均匀的硬币,恰好有两枚正面向上的概率为()



 使用微信扫一扫登录
使用微信扫一扫登录