函数y=f(x)的定义域为R,则下列函数为奇函数的是()
A. f(x)+f(-x)
B. f(x)-f(-x)
C. f(-x)f(x)
D. f(x2)
查看答案
相关试题
换一换


函数y=f(x)的定义域为R,则下列函数为奇函数的是()
A.f(x)+f(-x) B.f(x)-f(-x) C.f(-x)f(x) D.f(x2)
答案
下列函数在定义域内是奇函数又是增函数的是( )
A.y=log3x B.y=sinx C.y=x+8 D.y=x3
答案
下列函数在其定义域内,既是减函数又是奇函数的是( )
A. B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
下列函数在定义域内,既是奇函数又是增函数的是()。
A.y=sinx B.y=log2x C.y=x+8 D.y=x3
答案
下列函数在定义域内既是奇函数又是增函数的是( )。
A. B.
B. C.
C. D.
D.
 B.
B. C.
C. D.
D.
答案
下列函数中,即是奇函数又在定义域内递增的是()
A.f(x)=ex-e-x B.f(x)=2x+2-x C.f(x)= D.f(x)=ln|x|
答案
函数y=x在其定义域内既是奇函数又是增函数。
A.对 B.错
答案
下列函数中定义域为R的函数是( )。
A.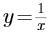 B.
B.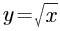 C.
C. D.
D.
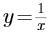 B.
B.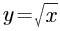 C.
C. D.
D.
答案
设函数f(x),g(x)的定义域均为R,且f(x)为奇函数,g(x)为偶函数,则下列说法正确的是()
A.f(x)+g(x)必为奇函数 B.f(x)+g(x)必为偶函数 C.f(x)g(x)必为奇函数 D.f(x)g(x)必为偶函数
答案
函数f(x)的定义域为R,若f(x+1)与f(x-1)都是奇函数,则( )
A.f(x)是偶函数 B.f(x)是奇函数 C.f(x)=f(x+2) D.f(x+3)是奇函数
答案
热门试题
下列函数定义域为R的是( )。
已知奇函数y=f(x)在其定义域上是增函数,那么y=f(-x)在它的定义域上()
1) 求函数 的定义域 ; 2) 求函数 的定义域 ; 3) 求函数 的定义域 ; 4) 求函数 的定义域 ./ananas/latex/p/238766
下列函数中,定义域为R的是().
正弦函数y=sinx在定义域R内是增函数。
函数f(x)的定义域是[0,1],则函数f(2x)的定义域是().
函数y=f(x)是定义域为R的增函数,则下列不等式中成立的是()
若函数f(x+1)的定义域是[-1,1],则函数f(x)的定义域是().
下列函数在定义域内是增函数的是( )。
下列函数在定义域内是减函数的是( )。
下列函数在定义域内为增函数的是( )。
分段函数的定义域是各分段区间的,它在其定义域上是函数。
已知定义域为R的函数f(x)在(8,+∞)上为减函数,且函数y=f(x+8)为偶函数,则( )。
已知定义域为R的函数f(x)在(8,+∞)上为减函数,且函数y=f(x+8)为偶函数,则( )。
函数f(x)的定义域为全体实数,且是以5为周期的奇函数,f(-2)=1,则f(12)等于()。
在定义域内下列函数中为增函数的是( )
在定义域内下列函数中为增函数的是()。
已知函数f(x)的定义域为R,则“f(x)为偶函数”是“f(-1)=f(1)”的
已知函数f(x)的定义域为R,则“f(x)为偶函数”是“f(-1)=f(1)”的().
已知函数f(2x)的定义域为(0,1),则函数f(x+1)的定义域为()



 使用微信扫一扫登录
使用微信扫一扫登录