当x=____时,函数y=x·2x取得极小值。
查看答案
相关试题
换一换


当x=( )时,函数y=x·2^x取得极小值。
A.ln2 B.-ln2 C.-1/ln2 D.1/ln2
答案
当x=____时,函数y=x·2x取得极小值。
答案
函数y=f(x)在点x=x0处取得极小值,则必有:()
A.f′(x0)=0 B.f″(x0)u003e0 C.f′(x0)=0且f″(x0)u003e0 D.f′(x0)=0或导数不存在
答案
函数y=f(x)在点x=x0处取得极小值,则必有:()
A.f′(x0)=0 B.f″(x0)>0 C.f′(x0)=0且f″(x0)>0 D.f′(x0)=0或导数不存在
答案
函数y =f(x)在点x=x0处取得极小值,则必有( )。
A.f"(x0)=0 B.f""(x0) > 0 C.f"(x0) = 0且f""(x0)>0 D.f"(x0)=0或导数不存在
答案
函数y=f(x)在点x=x0处取得极小值,则必有:
A.f′(x0)=0 B.f′′(x0)>0 C.f′(x0)=0 且 f(xo)>0 D.f′(x0)=0 或导数不存在
答案
求函数y=xex的极小值点与极小值
答案
函数f(x)=x3-3x的极小值为( )
A.-2 B.0 C.2 D.4
答案
函数f(x)=(x2-2)3+4的极小值为()。
A.f(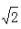 ) B.f(-
) B.f(-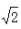 ) C.f(0) D.f(4)
) C.f(0) D.f(4)
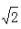 ) B.f(-
) B.f(-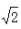 ) C.f(0) D.f(4)
) C.f(0) D.f(4) 答案
设函数(x)=ax3+bx2+x在x=1处取得极大值5.①求常数a和b;②求函数(x)的极小值.
答案
热门试题
函数f(x)=x3—12x的极小值点x=______.
已知f(x)=x3+ax2+bx在x=-1处取得极小值-2,则a=____,b=____。
已知f(x)=x^3+ax^2+bx在x=-1处取得极小值-2,则a=( ),b=( )。
二元函数z=x3-y3+3x2+3y2-9x的极小值点为( )
函数f(x,y)=x2-10x+y2+16y+100的极小值是().
求函数f(x)=x3-3x+5的极大值与极小值。
若f(x)和g(x)在x=x0处都取得极小值,则函数F(x)=f(x)+g(x)在x=x0处( )
设y=2x2+ax+3在点x=1处取得极小值,则a=()
可微函数f(x,y)在点(x0,y0)取得极小值,下列结论正确的是( ).
可微函数f(x,y)在点(x0,y0)取得极小值,下列结论正确的是( )。
设k>0,求函数f(x)=ln(1+2x)+kx2-2x的极值,并判断是极大值还是极小值.
设一个三次函数的导数为x2-2x-8,则该函数的极大值与极小值的差是:()
设f(x)=x3+ax2+bx在x=1处有极小值-2,则必有( )。
下列关于函数f①f(x)>0的解集是{x0<x<2};②f(-根号2)是极小值,f(根号2)是极大值;③f(x)没有最小值,也没有最大值()
在如下线性约束条件下:2x+3y<=30;x+2y>=10;x>=y;x>=5;y>=0,目标函数2x+3y的极小值为( )。
二元函数z=x3—y3+3x2+3y2—9x的极小值点为()
若f(x)=xex,则f(n)(x)的极小值点为().
设函数f(x)具有二阶连续导数,且f(x)>0,f"(0)=0,则函数z=f(x)lnf(y)在点(0,0)处取得极小值的一个充分条件是
若连续函数在闭区间上有极大值和极小值,则极大值必大于极小值。
当x=2时,函数y=-2x+1的值是()



 使用微信扫一扫登录
使用微信扫一扫登录