与向量(1,3,1)和(1,0,2)同时垂直的向量是( )。
A. (3,-1,0)
B. (6,-1,-3)
C. (4,0,-2)
D. (1,0,1)
查看答案
相关试题
换一换


与向量(1,3,1)和(1,0,2)同时垂直的向量是( )。
A.(3,-1,0) B.(6,-1,-3) C.(4,0,-2) D.(1,0,1)
答案
零向量与任何向量平行,也与任何向量垂直.
答案
向量a与向量b垂直,等价于向量a与向量b的数量积等于0.
答案
设a={2,2,1},b=(8,-4,1},则同时垂直于向量a与向量b的单位向量e=().
答案
设a、b、c均为非零向量,则与a不垂直的向量是:()
A.(a·C.b-(a·B.c B.B.b-(a·b/a·a C.a×b D.D.a+(a××a
答案
设a、b、c均为非零向量,则与a不垂直的向量是:()
A.(a·C.b-(a·B.c B.b-(a·b/a·a C.a×b D.a+(a××a
答案
设a、b、c均为非零向量,则与a不垂直的向量是()
A.(a·C.b-(a·B.c B.b-(a·b/a·a C.a×b D.a+(a××a
答案
设a,b,c为非零向量,则与a不垂直的向量是( )。
A.(a·c)b-(a·b)c B.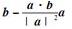 C.a×b D.a+(a×b)×a
C.a×b D.a+(a×b)×a
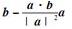 C.a×b D.a+(a×b)×a
C.a×b D.a+(a×b)×a 答案
向量→a与→b的负向量的和为向量→a与向量→b的差()
答案
已知向量a={2,1,-2)与向量b={3,-2,x)垂直,则x=().
答案
热门试题
已知向量a=(-1,2),b(m,1)若向量a+b与a垂直,则m=().
已知向量a=(-1,2),b=(m,1),
若向量a+b与a垂直,则m=( )
设向量a={2,-3,1},b={1,-2,3},则同时垂直于a和b,且在向量c={2,1,2}上投影为14的向量d=().
设向量x垂直于向量a= (2,3,-1)和b= (1, -2,3),且与c= (2,-1, 1)的数量积为-6,则向量x= ( )。
与向量 a=(2,3,1)垂直的平面是( )。
设向量x垂直于向量a=(2,3,-1)和b=(1,-2,3)且与c=(2,-1,1)的数量积为-6,则向量x=()
已知向量i,j为互相垂直的单位向量,向量a=2i+mj,若|a|=2,则m=()
设向量a={2,-1,2},向量b={0,3,-4},向量c={1,1,1},且3a+kb与c垂直,则常数k=().
设平面向量a=(2,1),b=(0,-2),则与a+2b垂直的向量可以是().
下列各对向量中垂直的是()
向量a(→)+2b(→)垂直于a(→)-4b(→),向量a(→)+4b(→)垂直于a(→)-2b(→),则a(→)与b(→)之间的夹角为( )。
下列各对向量中互相垂直的是()
若A经过初等行变换为B,则(): A的列向量组与B的列向量组等价|A的列向量组与B的行向量组等价|A的行向量组与B的列向量组等价|A的行向量组与B的行向量组等价
已知平面向量a=(-2,1)与b=(λ,2)垂直,则λ=()。
已知平面向量a(-2,1)与b= (A,2)垂直,则A=
已知平面向量ɑ=(-2,1)与b=(λ,2)垂直,则λ=( )
已知平面向量a=(-2,1)与b=(λ,2)垂直,则λ=( )
已知平面向量a,b满足|a|=|a-b|=2,向量b在向量a方向上的投影为3,则向量a与向量b的夹角为().
参数向量方程是包含参数和向量的方程。()
已知向量的终点坐标是,,其方向与向量的方向一致,则向量的起点坐标是



 使用微信扫一扫登录
使用微信扫一扫登录