#1=30 ;#2= COS[#1+15];G01 X[#2];则X的值为()
A. 1
B. 0.707
C. 2
查看答案
相关试题
换一换


#1=30 ;#2= COS[#1+15];G01 X[#2];则X的值为()
A.1 B.0.707 C.2
答案
设函数(x)=cos2x,则"(x)=().
A.2sin2x B.-2sin2x C.sin2x D.-sin2x
答案
设函数f(x)=cos2x,则f'(x)=()。
A.2sin2x B.-2sin2x C.sin2x D.-sin2x
答案
设函数f(x)=COS2x,则f′(x)=().
A.2sin2x B.-2sin2x C.sin2x D.-sin2x
答案
设函数f(x)=cos2x,则f'(x)=().
A.2sin2x B.-2sin2x C.sin2x D.-sin2x
答案
若f(x)=x2cos2x,则f(20)(0)=____。
答案
设f′(cos2x)=sin2x,则f(x)等于()
A.cosx+1/2cos2x+c B.cos2x-1/2cos4x+c C.x+(1/2)x2+c D.x-(1/2)x2+c
答案
若x=cos75°cos15°+sin75°sin15°,则x的值为()
A.1 B.0 C.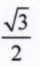 D.1/2
D.1/2
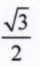 D.1/2
D.1/2 答案
G90 G01 X_ Z_ ×_;其中X、Z的值是表示()
A.终点坐标值 B.增量值 C.向量值 D.机械坐标值
答案
F[x]中,若f(x)g(x)=2,则f(x^2)g(x^2)=()
A.0 B.1 C.2 D.3
答案
热门试题
已知≤0<2π,且实数x满足log3x=2-cos2θ+sin2θ,则x的最小值是______。
函数y=2cosx-cos2x(x∈R)的最大值为______。
函数y=2cosx-cos2x(x∈R)的最大值为______。
F[x]中,若f(x)g(x)=2,则f(x^2)g(x^2)=(1.0分)
函数f(x)=3-2cos4x的最大值为()
函数y=2cos²x-sin²x的最大值为()
若f′(cos2x)=sinx,则f(x)等于:()
设函数y=cos2x,则y"=【】
设y=1+Cos2x,则y’=______。
设f(x)=ex,f[g(x)]=1-x2,则g(x)=____。
设f(x)的一个原函数为cos2x,则f(x)=()。
已知函数f(x)=sin2x+2cos2x-1.
(1)求f(x)的最小正周期;
(2)求f(x)的最大值及此时x的值.
已知多项式 f'(x)=x3—2x2-x+2,g(x)=x3+4x2+5x+2,则(f(x),g(x))=()。
函数f(x)=2sin3x的图象按向量a平移后得到的图象与g(x)=2cos3x的图象重合,则向量a可以是
已知x+x-1=2cos40°,则x4+x-4=()。
已知x+x-1=2cos40°,则x4+x-4=().
多项式f(x)=2x-7与g(x)=a(x-1)2+b(x+2)+c(x2+x-2)相等,则a,b,c的值分别为( )
设函数f(x)满足f'(sin2x)=cos2x,且f(0)=0,则f(x)=()
设函数f(x)=sinx,g(x)=x2,则f(g(x))()
当x→0时,1-cosx·cos2x·cos3x与axn为等价无穷小,求n与a的值。



 使用微信扫一扫登录
使用微信扫一扫登录