设向量a(→)={4,5,-3},b(→)={2,3,6},求a(→)对应的单位向量a(→)0以及b(→)的方向余弦,并求实数λ,μ满足什么条件才能使λa(→)+μb(→)与z轴垂直。
查看答案
相关试题
换一换


设向量a(→)={4,5,-3},b(→)={2,3,6},求a(→)对应的单位向量a(→)0以及b(→)的方向余弦,并求实数λ,μ满足什么条件才能使λa(→)+μb(→)与z轴垂直。
答案
设a、b都是单位向量,下列命题正确的是()。
A.a=b B.若a∥b,则a=b C.a2=b2 D.a·b=1
答案
设a={2,2,1},b=(8,-4,1},则同时垂直于向量a与向量b的单位向量e=().
答案
已知向量a,b是夹角为60°的单位向量,则|a+b|=()
A.1 B.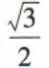 C.
C.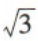 D.
D.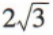
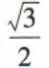 C.
C.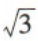 D.
D.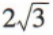
答案
设i,j,k为单位向量且互相垂直,向量a=i+j,b=-i+j-k,则a·b=_____.
答案
若向量a,b均为单位向量,且它们的夹角为60°,则|a+2b|=()
A.√3 B.√5 C.√7 D.2√2
答案
向量( )是单位向量。
A.(1,1,-1) B.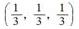 C.(-1,0,0) D.
C.(-1,0,0) D.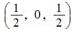
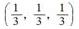 C.(-1,0,0) D.
C.(-1,0,0) D.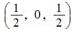
答案
已知i,j,k为单位向量且互相垂直,向量a=i+j,b=-i+j-k,则a·b=()。
答案
已知平面向量a,b且满足a▪b=|a|=|b|=2,若e为平面单位向量,则|a▪e+b▪e|的最大值为().
A.3 B.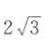 C.4 D.
C.4 D.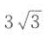
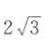 C.4 D.
C.4 D.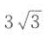
答案
若a,b为单位向量且互相平行,则它们的数量积a·b=()
A.1 B.-1 C.0 D.1或-1
答案
热门试题
已知两个单位向量a,b的夹角是120°,则|a-b|=()
两个单位向量的叉积还是单位向量()
已知a,b是单位向量,则下列结论中正确的是()
两个单位向量相加一定不是单位向量
设三向量a(→),b(→),c(→)满足关系a(→)+b(→)+c(→)=0,则a(→)×b(→)=( )。
设a={2,3,5),b={-3,4,0},则向量a在向量b上的投影为()
向量a与向量b垂直,等价于向量a与向量b的数量积等于0.
是单位向量.
设平面向量a=(2,1),b=(0,-2),则与a+2b垂直的向量可以是().
设向量a={-1,-3,6},b={4,-3,0},则a×b=().
已知向量a,b满足|a|=1,|b|=2,a·(a+b)=0,则向量a与b的夹角为()
已知向量口=(2,1),b=(X,Y)。
(1)若X∈{-1,0,1,2),Y∈{-1,0,1),求向量a//b的概率;
(2)若X∈[-1,2],Y∈[-1,1],求向量a,b的夹角是钝角的概率。
下列四个向量中,不是单位向量的是()
下列四个向量中,不是单位向量的是()
设α=(-1,2,2),则与α反方向的单位向量是 _________________
已知向量a=(3,4),向量 b=(0,-2),则cos的值为()
已知向量口=(2,1),b=(X,Y)。 (1)若X∈{-1,0,1,2),Y∈{-1,0,1),求向量a//b的概率; (2)若X∈[-1,2],Y∈[-1,1],求向量a,b的夹角是钝角的概率。
设α=i+k,β=-j+k,与α,β都垂直的单位向量为( )。
已知平面向量a=(-1,2),b=(1,0),则向量3a+b=().
若|a|=1,|b|=7,且向量a、b垂直,求|(a+b)×(a-b)|.



 使用微信扫一扫登录
使用微信扫一扫登录