已知集合P={-1,0,1,3,4,6},Q={-2,-1,4,5},则PnQ=()
A. {-2,0}
B. {-1,3}
C. {0,3,6}
D. {-1,4}
查看答案
相关试题
换一换


已知集合P={-1,0,1,3,4,6},Q={-2,-1,4,5},则PnQ=()
A.{-2,0} B.{-1,3} C.{0,3,6} D.{-1,4}
答案
已知“P←→q”、“P∧q”、“P→q”均真,则().
A.P真q真 B.P假q假 C.P真q假 D.非P真非q假
答案
已知文法G[S]:S→P|S+P|S-P,P→Q|P*Q|P/Q,Q→(S)|a,该文法的终结符号集合VT是()。
A.VT={+、*、/、(、)、a} B.VT={-、*、/、(、)、a} C.VT={+、-、*、/、(、)、a} D.VT={+、-、*、/、(、)、a}
答案
设集合P=(1,2,3,4,5),Q={2,4,6,8,10},则集合P∩Q=()。
A.{2,4} B.{1,2,3,4,5,6,8,10} C.{2} D.{4}
答案
[0501]设集合P=(1,2,3,4,5),Q={2,4,6,8,10},则集合P∩Q=()
A.{2,4) B.{1,2,3,4,5,6,8,10) C.{2} D.{4}
答案
已知“当且仅当p才q”、“p∧q”、“p→q”均真,则()
A.p假q真 B.p真q真 C.p真q假 D.非p真非q 假
答案
已知p→q为假,则p和q的真值为()。
A.p真并且q真 B.p真并且q假 C.p假并且q真 D.p假并且q假
答案
已知p∧q为假,则p和q的真值为()、()、()
答案
已知p→q为假,则p和q的真值为()
答案
集合P={3的倍数},Q={6的倍数},则P与Q之间的关系是()
A.P=Q B. C.
C.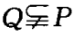 D.P∩Q= P
D.P∩Q= P
 C.
C.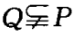 D.P∩Q= P
D.P∩Q= P 答案
热门试题
已知集合P={1,x,y},Q={x,x2,xy},若P=Q,求x,y的值.
已知p:│x│=x,q:x²≥-x,则p是q的( )条件
已知P是q的充分条件,则q是P的()
已知p要么q为假,则p和q的真值为()、()
已知p←q为假,则P与q的取值情况必为()。
已知P∧q为真,则()为假。
已知“p∧q”为真,则()、()、()为假
已知P是q的充分条件,则
已知p:|2x—3|<1,q:x(x—3)<0,则p是q的()
已知“p并且q”、“p或是q”均取假值,则下列为假的判断形式是()。
已知p:|3x-5|<4,q:(x-1)(x-2)<0,则p是q的().
已知P={x∈N|a>x>2},已知集合P中恰有3个元素,则整数a=( )。单项选择题选项:
已知“当且仅当p则q”为真,则其肢判断().
已知:命题P:x+y>2且xy>1,命题Q:x>1且y>1,则Q是P的()
已知有变量定义: double* p , q ; 则变量的类型情况是:
已知RSA算法选取的大素数分别为p和q,n=p*q,则欧拉函数值为()
巳知 “ p ← q ”“ p ∧ q ”,“ p → q ”均真,则
巳知“p←q”“p∧q”,“p→q”均真,则()
设 p,q 是指针,若 p=q,则*p=*q
设X是随机变量,已知P(X≤1)=p,P(X≤2)=q,则P(X≤1,X≤2)等于( ).



 使用微信扫一扫登录
使用微信扫一扫登录