若F′(x)=f(x),即F(x)是f(x)的一个原函数,则下列等式中哪一个可以成立?()
A. F′(x)dx=f(x)+c
B. f(x)dx=F(x)+c
C. F(x)dx=f(x)+c
D. f′(x)dx=F(x)+c
查看答案
相关试题
换一换


若F′(x)=f(x),即F(x)是f(x)的一个原函数,则下列等式中哪一个可以成立?()
A.F′(x)dx=f(x)+c B.f(x)dx=F(x)+c C.F(x)dx=f(x)+c D.f′(x)dx=F(x)+c
答案
若?是?的一个原函数,则?(???????)?
答案
设f(x)的一个原函数为xln(x+1),则下列等式成立的是()。
A.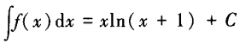 B.
B.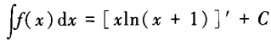 C.
C.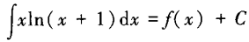 D.
D.
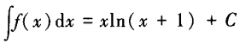 B.
B.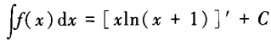 C.
C.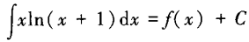 D.
D.
答案
若f (x)的一个原函数是lnx/x,则 ( )。
A.lnx/x+C B.(1+Inx) /x+C C.1/x+C D.(1- 2lnx) /x+C
答案
若f(χ)的导函数是sinχ,则f(χ)有一个原函数为( )。
A.1+sinχ B.1-sinχ C.1+cosχ D.1-cosχ
答案
若f(x)的导函数是cosx,则函数f(x)有一个原函数是()
A.1+sinx B.1-sinx C.1+cosx D.1-cosx
答案
设F(x)是f(x)的一个原函数,则∫e
-xf(e
-x)dx等于下列哪一个函数?()
A.F(e -x)+c B.-F(e -x)+c C.F(e x)+c D.-F(e x)+c
答案
若1/X是,f(x)的一个原函数,则f,(x)=——.
答案
若f(x)的一个原函数是()
A.4cos4x+C B. C.4cos2x+C D.8cos4x+C
答案
若f(x)的一个原函数是()
A.4cos4x+C B.4cos2x+C C.8cos4x+C
答案
热门试题
若f(x)的一个原函数为xlnx,则f’(x)=()。
设F(x)是f(x)的一个原函数,则∫e-xf(e-x)dx等于下列哪一个函数?()
下列函数中,哪一个不是f(x)=sin2x的原函数?
若e-x是f(x)的一个原函数,则∫xf(x)dx=____。
(2010)若函数f(x)的一个原函数是e-2x,则∫f″(x)dx等于:()
若f(x)的导函数是e-x+cosx,则f(x)的一个原函数为( )。
若f(x)的一个原函数是e-2x,则?f'(x)dx= ( )。
若f(x)的一个原函数是e-2x,则∫f""(x)dx= ( )。
若e-7x+cos3x+2x-2是函数f(x)的一个原函数,则f'(x)的全体原函数是().
若f(x)的一个原函数为x2,则/ananas/latex/p/234676
设 是 的一个原函数,则/ananas/latex/p/19792
设f(x)的一个原函数为cosx,g(x)的一个原函数为x2,则f[g(x)]等于:()
设F(x)是f(x)的一个原函数,则等于()。
设x是f(x)的一个原函数,则f(x)=()。
设x是f(x)的一个原函数,则f(x)=()。
设f(x)的一个原函数是arctanx,则f(x)的导函数是()
证明:连续的奇函数的一切原函数皆为偶函数;连续的偶函数的原函数中只有一个是奇函数。
若F(x)是f(x)的一个原函数,G(x)是1/f(x)的一个原函数,且F(x)G(x)=-1,f(0)=1,求f(x)。
若函数f(x)在(a,b)内存在原函数,则原函数有()。
同一个函数的原函数只差一个常数。



 使用微信扫一扫登录
使用微信扫一扫登录