直线的一般式方程为Ax+By+c=0(A,B不同时为0)。
查看答案
相关试题
换一换


直线的一般式方程为Ax+By+c=0(A,B不同时为0)。
A.对 B.错
答案
过点(0,1)且与直线2x-y=0垂直的直线方程的一般式是y=-2x+1。()
答案
经过点(-3,0)且倾斜角为135°的直线的一般式方程是( )。
A.x-y-3=0 B.x-y+3=0 C.x+y=3 D.x+y+3=0
答案
把直线方程y=0.5x+m化为一般式方程是x-2y-8=0,则m的值为( )。
A.-8 B.-4 C.4 D.8
答案
空间一般力系有∑X=0,∑Y=0,∑Z=0,∑Mx=0,∑My=0,∑Mz=0六个平衡方程,若有一个在xy平面内的平面一般力系,则其平衡方程是()。
A.∑X=0,∑Y=0,∑Mx=0 B.∑X=0,∑Y=0,∑My=0 C.∑X=0,∑Y=0,∑Mz=0 D.∑X=0,∑Z=0,∑Mz=0
答案
已知A(2,-3),B(3,-2),直线l的方程为mx+y+1=0,若直线l//AB,则m=()
A.-1 B.1 C.-2 D.2
答案
目前一般认为AB0血型基因是()
A.等位基因 B.二复等位基因 C.三复等位基因 D.四复等位基因 E.五复等位基因
答案
平面一般力系,其独立的二力矩式平衡方程为?∑Fx=0,∑MA=0,∑MB=0,但要求矩心A、B的连线不能与x轴垂直。( )
答案
把直线方程y-2=-(x+3)化为一般式方程是( )。
A.x+y-1=0 B.x+y+1=0 C.x-y-1=0 D.x-y+1=0
答案
把直线方程y-2=-(x+3)化为一般式方程是( )。
A.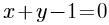 B.
B.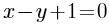 C.
C. D.
D.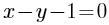
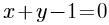 B.
B.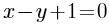 C.
C. D.
D.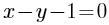
答案
热门试题
把直线方程y-2=2(x+3)化为一般式方程是( )。
过点(0,1)且与直线x+y+1=0垂直的直线方程为( )
过点(0,1)且与直线x+y+1=0垂直的直线方程为()
经过点(0,-4)且斜率为2的直线的斜截式方程是( )。
经过点(0,3),倾斜角为0°的直线方程为()
过点(-1,0)与直线x-y-2=0平行的直线的方程为( )。
过点(0,1)且与直线x-y+2=0平行的直线方程为()
过直线x+y+1=0和直线x-2y+4=0的交点,且与直线x+2y-3=0垂直的直线方程是()
过点(1,0)且与直线x+2y-3=0平行的直线方程是( )。
已知点A(1,0),B(-1,1),若直线kx-y-1=0与直线AB平行,则k=()
已知点A(1,0),B(-1,1),若直线kx-y-1=0与直线AB平行,则k=()
过A(3,0),B(0,2)两点的直线的方程为()
过点(1,0)且与直线x-2y-2=0平行的直线的方程是()
y轴所在的直线的方程是y=0。
平面一般力系平衡方程式的其中一种:∑Px=0,∑MA(p)=0,∑MB(p)=0,A、B连线必须平行x轴()
设直线方程为x=y-1=z, 平面方程为:x一2y+z=0,则直线与平面()
过直线2x-y+4=0与x-y+5=0的交点,且垂直于直线x-2y=0的直线的方程为()
若直线l与直线4x-3y+2=0平行,且过点(0,3),则直线l的方程为( )。
经过圆x2+2x+y2=0的圆心,与直线x+y=0垂直的直线方程是( )。
过点P(-2,0),且平行于向量v(0,3)的直线方程是________.



 使用微信扫一扫登录
使用微信扫一扫登录