若点(4,-3)到直线3x-4y+m=0的距离为5,则m的值为( )。
A. -49或1
B. -1
C. 1
D. -49
查看答案
相关试题
换一换


若点(4,-3)到直线3x-4y+m=0的距离为5,则m的值为( )。
A.-49或1 B.-1 C.1 D.-49
答案
已知点P(-2,1)到直线l:3x-4y+m=0的距离为1,则m的值为()
A.-5或-15 B.-5或15 C.5或-15 D.5或15
答案
若点(4,a)到直线4x-3y-1=0的距离不大于3,则a的取值范围是( )
A.(0,10) B.[0,10] C.(10,30) D.(-10,10)
答案
点M(3,-2)到直线2x+3y+5=0的距离是3。
A.对 B.错
答案
点(2,1)到直线4x-3y+5=0的距离为( )。
A.4 B.3 C.2 D.1
答案
已知过点 A(m+1,0),B(-5,m)的直线与过点 C(-4,3),D(0,5)的直线平行,则m的值为()
答案
P(2,a)为第一象限内的点,且到直线4x-3y+2=0的距离等于4,则a的值是()
A.4 B.6 C.8 D.10
答案
已知点(a,-3)(a>0)到直线 l:x−y−2=0的距离为1,则a等于()
A.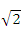 B.
B.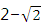 C.
C.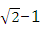 D.
D.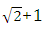
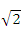 B.
B.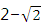 C.
C.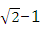 D.
D.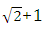
答案
点(-2,3)到直线l:3x+4y+3=0的距离是()
A.2 B.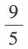 C.
C.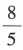 D.
D.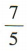
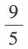 C.
C.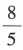 D.
D.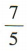
答案
过点P(m,4)和点Q(1,m)的直线与直线x-2y+4=0平行,则m的值为()
答案
热门试题
若直线2x-3y+4=0与2x+my-8=0平行,则m=( )。
若直线2x-3y+4=0与2x+my-8=0平行,则m=( )。
点(3,5)到直线4y=3x+1的距离是( ).
圆x²+y²−2x+4y+4=0上的点A到直线3x−4y+9=0的最大距离等于( )
若直线l与直线4x-3y+2=0平行,且过点(0,3),则直线l的方程为( )。
求点M(1,2,1)到平面3x-4y+5z+2=0的距离()
设P为x轴上一点,P到直线3x-4y+6=0的距离为6,则P点坐标为________.
已知过点A(a,3),和B(4,5)的直线与直线2x-y+1=0平行,则a的值为( )
点(2,1,0)到3x+4y+5z=0的距离d=____.
若直线x+ay-3=0与直线2x-y+1=0垂直,则a的值为( )。
若直线mx+4y-2=0与直线2x-5y-12=0垂直,则实数m的取值为()
已知点A(1,3)和点B(m,0)的距离为5,则m的值为( )。
点(2,1,0)到平面3x+4y+5z=0的距离d=____。
已知两点O(0,0),A(4.-1)到直线mx+m2y+6=0距离相等,则实数m可取的不同值共有()
若直线3x+4y+k=0与圆x2+y2-6x+5=0相切,则k的值等于()
已知圆的方程为x2+y2-2x+4y+1=0,则圆上一点到直线3x+4y-10=0的最大距离为()
已知圆的方程为x2+y2-2x+4y+1=0,则圆上一点到直线3x+4y-10=0的最大距离为( )
点M(-2,20)到直线2x-7=0的距离为( )。
若过点P(-1,3)和点Q(1,7)的直线l₁与直线l₂:mx+(3m-7)y+5=0平行,则m的值为()
若点P(x,y)在直线x+y-4=0上,O为原点,则|OP|的最小值是()



 使用微信扫一扫登录
使用微信扫一扫登录