设a,b,c为三个向量,若a·b=a·c,则()。
A. b=c
B. a⊥b且a⊥c
C. a=0或b-c=0
D. D.a⊥(b-
查看答案
相关试题
换一换


设a,b,c为三个向量,若a·b=a·c,则()。
A.b=c B.a⊥b且a⊥c C.a=0或b-c=0 D.D.a⊥(b-
答案
设a,b,c为三个向量,若a·b=a·c,则()。
A.b=c B.a⊥b且a⊥c C.a=0或b-c=0 D.a⊥(b-
答案
设a,b,c为三个向量,若a·b=a·c,则()。
D.a⊥(b-C.
答案
设ABC为三个事件,则ABC同时发生可表为()。
A.A∩B∩Cbr/> B.A∪B∪ C.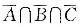 D.
D.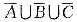
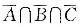 D.
D.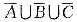
答案
设α、β、γ均为三维列向量,以这三个向量为列构成的3阶方阵记为A,即A=(αβγ)。若α、β、γ所组成的向量组线性相关,则 A 的值是( )。
A.大于0 B.等于0 C.大于0 D.无法确定
答案
设α,β,γ都是非零向量,若α×β=α×γ,则()。
A.β=γ B.α//β且α//γ C.α//(β-γ) D.α⊥(β-γ)
答案
设ɑ、β、γ都是非零向量,若ɑⅹβ=aⅹγ,则()。
A.β=γ B.ɑ//β 且ɑ//γ C.ɑ// (β-γ) D.ɑ⊥(β-γ)
答案
设α,β,γ都是非零向量,若α×β=α×γ,则()
A.β=γ B.α//β且α//γ C.α//(β-γ) D.α⊥(β-γ)
答案
设α、β、γ都是非零向量,若α×β=α×γ,则()
A.β=γ B.α∥β且α∥γ C.α∥(β-γ) D.α⊥(β-γ)
答案
设α,β, r都是非零向量,若αxβ=αxy, 则()
A.β=y B.αllβ且αllγ C.αll(β-y) D.a⊥(β-y)
答案
热门试题
三个向量线性相关的几何意义是三个向量共面。
中国大学MOOC: 对任意三个向量 a,b,c 和任意三个实数 l,m,n,则三个向量la-m b , m b-nc , nc-la 共面.
设向量a=(x,4),b=(2,-3),若a·b=2,则x=()
设向量a=(x,2),b=(6,3).若a//b,则x=()
设A,B,C是△ABC的三个内角,下列关系恒成立的是().
设向量a=(2,3sinθ),b=(4,cosθ),若a//b,则tanθ=()
设向量a=(t,-6),b=(-3,2).若a//b,则实数为()
设A是三阶实对称矩阵,若对任意的三维列向量X,有X^TAX=0,则()
设A是三阶实对称矩阵,若对任意的三维列向量X,有X^TAX=0,则()
设A是三阶实对称矩阵,若对任意的三维列向量X,有X^TAX=0,则().
设三向量a,b,c满足关系a·b=a·c,则( ).
已知三维列向量a,β满足aTβ,设3阶矩阵A=βaT,则:
设α1,α2,α3,α4 是三维实向量,则( )
三个非零向量共面,则下列结论不一定成立的是()。
设三向量a,b,c满足关系式a·b=a·c,则()
设三向量a(→),b(→),c(→)满足关系a(→)+b(→)+c(→)=0,则a(→)×b(→)=( )。
设三向量a,b,c满足关系式a·b=a·c,则()
一个中心位于参考坐标系原点的坐标系由三个向量表示,通常着三个向量相互垂直
某平面力系由三个力组成,设这三个力互不平行,则正确的有()
设α,β,γ都是非零向量,α×β=α×γ,则()。



 使用微信扫一扫登录
使用微信扫一扫登录