高职单招数学考试试题
考试总分:100分
考试类型:模拟试题
作答时间:120分钟
已答人数:1553
试卷答案:有
试卷介绍: 为各位正在备考的小伙伴带来了高职单招数学考试试题,还有答案解析可以在线查看。
试卷预览
-
1. 过直线x+y=2与x-y=0的交点,且法向量n=(-2,3)的直线方程是()
A-3x+2y+1=0
B3x-2y+1=0
C-2x+3y+1=0
D2x-3y+1=0
-
2. 设直线l1:x-y+1=0;l2:3x-y-1=0,那l1与l2夹角的正切是()
A2
B4
C1/2
D1
-
3.
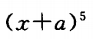 展开式的第5项为125x,则a等于()。
展开式的第5项为125x,则a等于()。A5
B±5
C
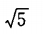
D
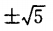
-
4. 若
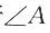 与
与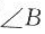 的两边分别平行,
的两边分别平行,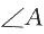 =50°,则
=50°,则 =().
=(). A40°
B50°
C40°或140°
D50°或130°
-
5. 在△ABC中,已知B=60°,b2=ac,那么△ABC是().
A等腰三角形
B等边三角形
C直角三角形
D等腰直角三角形
-
6. 在△ABC中,
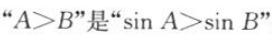 的().
的().A充分不必要的条件
B必要不充分条件
C充要条件
D既不充分也不必要条件
-
7. 抛物线
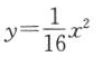 的焦点坐标是().
的焦点坐标是(). A(0,2)
B(0,4)
C(0,8)
D(0,16)
-
8. 动点到点(3,0)的距离比它到直线x=-2的距离大1,则动点的轨迹是().
A椭圆
B双曲线
C双曲线的一支
D抛物线
-
9. 已知两条直线ax-y-2=0和(a+2)x-y+1=0互相垂直,则a等于().
A-1
B0
C1
D2
-
10. 若函数f(x)同时满足下列三个性质:①最小正周期为π;②图像关于直线
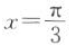 对称;③在区间
对称;③在区间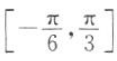 上是增函数.则f(x)的解析式可以是().
上是增函数.则f(x)的解析式可以是().A
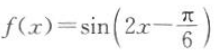
B

C
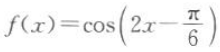
D
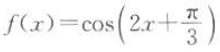
-
11. 若
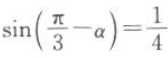 ,则
,则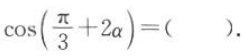
A
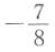
B
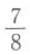
C
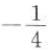
D
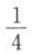
-
12. 垂直于x轴的直线交抛物线y²=12x于点A,B且|AB|=
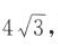 ,则直线AB的方程为().
,则直线AB的方程为().Ax=1
Bx=-1
Cy=1
Dy=-1
-
13. 已知函数f(x)是定义在R上的奇函数,且对于任意实数x都有f(x+4)=f(x).若f(-1)=3,则f(4)+f(5)=().
A-3
B0
C3
D6
-
14. 已知扇形的中心角为
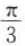 ,半径为2,则其面积为(),
,半径为2,则其面积为(),A
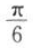
B
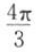
C
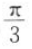
D
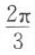
-
15. 某函数的大致图像如图所示,则该函数可能是().
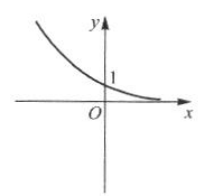
Ay=2-x
By=2x
Cy=-2x
Dy=-2-x
-
16. 直线l:mx-y+1-m=0与圆C:x2+(y-1)2=5的位置关系是().
A相交
B相切
C相离
D不确定
-
17. 过点(1,0)与点(2,2)的直线方程为().
A2x-y-2=0
B2x-y+1=0
Cx-2y-1=0
Dx-2y+2=0
-
18. 数列
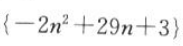 中的最大项是()
中的最大项是()
A107
B108
C
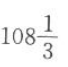
D109
-
19. 等差数列
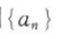 中, a1+a4+a7=39,a3+a6+a9=27,则数列
中, a1+a4+a7=39,a3+a6+a9=27,则数列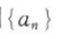 的前9项和S9,等于( ).
的前9项和S9,等于( ).
A66
B99
C144
D297
-
1.
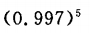 精确到千分之一的近似值为_______.
精确到千分之一的近似值为_______.
-
2. 若直线kx-y-3=0与圆
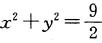 相切,则k=________;切点坐标是________.
相切,则k=________;切点坐标是________.
-
3.

-
4. 从1,2,3,4.5,6,7七个数中任取两个数相乘,使所得的积为偶数,这样的偶数共有()个.
-
5. 已知△ABC内角A,B,C所对的边分别为a,b,c,若a=3,b=2,A=60°,则cos B=().
-
6. 在数列{an}中,a1=3,
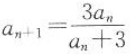 ,则a4=().
,则a4=().
-
1. 加工某一零件共需经过三道工序,设第一、二、三道工序的次品率分别为2%、3%、5%,假定各道工序是互不影响的,问加工出来的零件的次品率是多少?
-
2. 已知线段AB(AB=2a)的两个端点A和B分别在x轴、y轴上滑动,求线段AB的中点M的轨迹方程.
-
3. 计算:
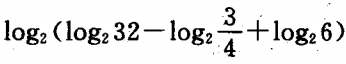
-
4. 已知集合
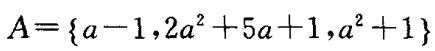 ,且
,且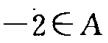 ,求实数a的值。
,求实数a的值。
-
5. 求和:Sn=1×2+2×3+3×4+…+n(n+1).
-
6. 已知:
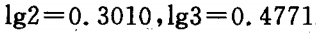
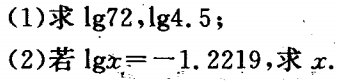
-
2022年高职单招每日一练《数学》10月8日1297人做过
-
2022年高职单招每日一练《数学》10月9日1283人做过
-
2022年高职单招每日一练《数学》10月10日1294人做过
-
2022年高职单招每日一练《数学》10月11日1896人做过
-
2022年高职单招每日一练《数学》10月12日1784人做过
-
2022年高职单招每日一练《数学》10月13日1743人做过
-
2022年高职单招每日一练《数学》10月14日1200人做过
-
2022年高职单招每日一练《数学》10月15日1264人做过
-
2022年高职单招每日一练《数学》10月16日1691人做过
-
2022年高职单招每日一练《数学》10月17日1559人做过