2024年成人高考高起点数学(文史)模拟试卷及答案(二)

• 1. 设集合M={a，b，c，d}，N=（a，b，c），则集合M∪N=（）。  

  A{a，b，c}

  B{d}

  C{a，b，C，d}

  D空集

• 2. 已知集合M：（0，1，2），则M的真子集的个数为（）。  

  A4个

  B5个

  C6个

  D7个

• 3. 设命题甲：x+1=0，命题乙：x²-2x-3=0，则（）。  

  A甲是乙的充分条件，但不是乙的必要条件

  B甲是乙的必要条件，但不是乙的充分条件

  C甲是乙的充分必要条件

  D甲不是乙的必要条件，也不是乙的充分条件

• 4. 不等式-2x²+3＜5x的解集是（）。  

  A空集

  B{x|-3＜x＜}

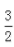  C全体实数

  D{x|x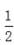＞或x＜-3}

• 5. 若A（-3，5），B（-5，-3），则线段AB中点的坐标为（）。  

  A（4，-1）

  B（-4，1）

  C（-2，4）

  D（-1，2）

• 6. 函数f（x）=x³-6x²+9x-3的单调区间为（）。  

  A（-∞，-3），（-3，1），（1，+∞）

  B（-∞，-1），（-1，3），（3，+∞）

  C（-∞，-3），（-3，-1），（-1，+∞）

  D（-∞，1），（1，3），（3，+∞）

• 7. 已知向量|a|=3，|b|=4，且a和b的夹角为120°，则a·b=（）。

  A

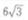
  B

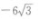
  C6

  D-6

• 8. 若|a|=|b|=1，且a⊥b，又2a+3b与λa-4b互相垂直，则λ为（）

  A6

  B-6

  C3

  D-3

• 9. （）。

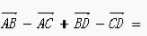  A

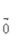
  B

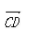
  C

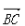
  D

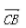
• 10. 已知等比数列a₁=1，a₉=25，则a₅=（）。

  A25

  B-5

  C±5

  D5

• 11. 某车间有甲、乙两台机床，已知甲机床停机的概率为0.06，乙机床停机的概率为0.07，甲、乙两车床同时停机的概率是（）。

  A0.13

  B0.0042

  C0.03

  D0.04

• 12. 在自然数1、2、…、100中任取一个数能被3整除的概率是（）。

  A

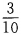
  B

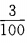
  C

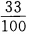
  D

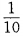
• 13. 下列各等式不成立的是（）。

  A3^x·2^x=6^x

  B9^x=（3^x）²

  C

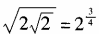
  D

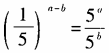
• 14. 已知tanα，tanβ是方程2x²-4x+1=0的两根，则tan（α+β）=（）。

  A4

  B-4

  C

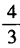
  D8

• 15. 已知3sin²α+8sinα-3=0，则cos2α=（）。

  A

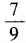
  B

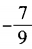
  C

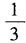
  D

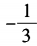
• 16. 已知x+x^-1=2cos40°，则x⁴+x^-4=（）。

  A2cos20°

  B-2cos20°

  C2sin80°

  D-2sin80°

• 17. 设集合M=｛-2，0，2｝，N=｛0｝，则（）。  

  AN为空集

  BN∈M

  C

  D

• 1. 一个问题在1小时内，甲能独立解决的概率是0.5，乙能独立解决的概率是0.4，两人在1小时内解决问题的概率是______。

• 2. 某人投篮每次命中率为0.8，现独立投篮4次，恰好命中3次的概率是______。  

• 3. =______。

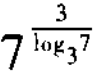• 4. 已知点P（-3，1）为角α终边上一点，则cos（2α-π）的值等于______。  

• 1. 弹簧的身长与下面所挂砝码的重量成正比，知弹簧挂20g重的砝码时长度是12cm,挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度

• 2. 求（1+tan10°）（1+tan35°）的值。

• 3. 设函数 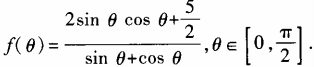（1）求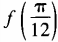；（2）求函数f（θ）最小值。