2024年成考高起点每日一练《数学(理)》10月5日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:985
试卷答案:有
试卷介绍: 2024年成考高起点每日一练《数学(理)》10月5日专为备考2024年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 5名高中毕业生报考3所院校,每人只能报一所院校,则有()种不同的报名方法
A
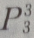
B
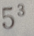
C
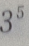
D

-
2. 抛物线y2=2px上任意一点与焦点连线中点的轨迹方程是()。
A
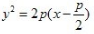
B
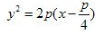
C

D
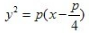
-
3. 设双曲线
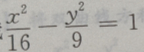 的渐近线的斜率为k,则|k|=()
的渐近线的斜率为k,则|k|=()
A
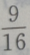
B
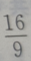
C
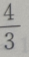
D
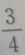
-
4. 若
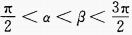 ,则必有()。
,则必有()。Asinα>sinβ
Bcosα>cosβ
Ctanα>tanβ
Dcotα>cotβ
-
1. 如图
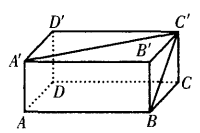 ,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
,已知长方体的长和宽都是4cm,高是2cm。求 (1)BC和A’C’所成的角是多少度?
(2)A’B’和DD’的距离是多少?
-
2. 设
 分别讨论x→0及x→1时f(x)的极限是否存在?
分别讨论x→0及x→1时f(x)的极限是否存在?
-
3. 已知关于x的二次方程
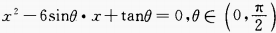 的两根相等,求sinθ+cosθ的值。
的两根相等,求sinθ+cosθ的值。
-
4. 设A1A2A3A4A5A6为正六边形,如图
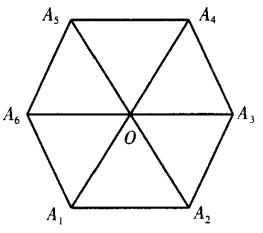 ,O为它的中心。 (1)求证:
,O为它的中心。 (1)求证: 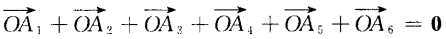 (2)
(2)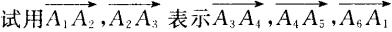
-
1. ABCD是正方形,E是AB的中点,如将△DAE和△CBE分别沿虚线DE、CE折起,使AE与BE重合如图
 ,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
,设A与B重合后的点为P,则面PCD与面ECD所成的二面角为______度,PE与面ECD成______度。
-
2. 已知
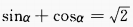 ,则
,则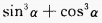 =______。
=______。
相关试卷
-
2022年成考高起点每日一练《数学(理)》10月24日1201人做过
-
2022年成考高起点每日一练《数学(理)》10月25日1542人做过
-
2022年成考高起点每日一练《数学(理)》10月26日1324人做过
-
2022年成考高起点每日一练《数学(理)》10月27日1379人做过
-
2022年成考高起点每日一练《数学(理)》10月28日1924人做过
-
2022年成考高起点每日一练《数学(理)》10月29日347人做过
-
2022年成考高起点每日一练《数学(理)》10月30日232人做过
-
2022年成考高起点每日一练《数学(理)》10月31日1105人做过
-
2022年成考高起点每日一练《数学(理)》11月1日1743人做过
-
2022年成考高起点每日一练《数学(理)》11月2日1480人做过
相关题库