2024年成考高起点文科数学全真模拟卷(三)

• 1. 直线2x-y+7=0与圆(x-1)²+(y+1)²=20的位置关系是（）。

  A相离

  B相交但不过圆心

  C相切

  D相交且过圆心

• 2. 椭圆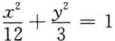的焦点是F1和F2，点P在椭圆上，△PF1F2的周长是（）。

  A

  B18

  C15

  D

• 3. 若函数ƒ(x)=1+log_ax在(0，+∞)上是减函数，则（）。

  Aa>1

  Ba>2

  C1

  D0

• 4. 不等式2x²＋3mx＋2m＞0的解集是实数集，则m的取值范围是（）。

  Am＜16/9

  Bm＞0

  C0＜m＜16/9

  D0≤m≤16/9

• 5. 已知函数f(χ)=ax²+b的图像经过点(1，2)，且其反函数f^-1(χ)的图像经过点(3，0)，则函数f(χ)的解析式是（）。

  Af(χ)=1/2x²+3/2

  Bf(χ)=-χ²+3

  Cf(χ)=3χ²+2

  Df(χ)=χ²+3

• 6. 函数 f(x)=x(1/2^x−1+1/2) (x∈R且x≠0)（）。

  A是偶函数

  B既是奇函数又是偶函数

  C既不是奇函数，也不是偶函数

  D是奇函数

• 7. 0.7²,log₂0.7, 2^0.7三个数之间的大小关系是（）。

  A0.7²＜2^0.7＜log₂0.7

  B0.7²＜log₂0.7＜2^0.7

  Clog₂0.7＜0.7²＜2^0.7

  Dlog₂0.7＜2^0.7＜0.7²

• 8. 设集合P＝｛x|－1≤x≤3｝，N＝｛x|2≤x≤4｝，则P∪N是（）。

  A｛x|2≤x≤3｝

  B｛x|2＜x＜3｝

  C｛x|-1＜x＜4｝

  D｛x|-1≤x≤4｝

• 9. 在△ABC中，三边为a、b、c，∠B=60°，则a²-ac+c²-b²的值是()。

  A大于零

  B小于零

  C等于零

  D不能确定

• 10. 函数ƒ(x)=x(5^x-5^-x)是()。

  A既不是奇函数又不是偶函数

  B奇函数

  C偶函数

  D既是奇函数，又是偶函数

• 11. 在等差数列{an｝中，已知a1+a2+a3+a4+a5=15，则a3=()。

  A3

  B4

  C5

  D6

• 12. 设log₃7=a，则log₇27=()。

  A-3a

  B3a^-1

  C3a

  D2a

• 13. 下列函数中为偶函数，且在区间(0，+∞)上是减函数的是（）。

  Ay=log₃x²

  By=x²-x

  Cy=-3^｜x｜

  D

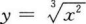
• 14. 等差数列{a_n}中，已知a₅+a₈=5，那么a₂+a₁₁的值等于（）。

  A5

  B10

  C15

  D20

• 15. 已知向量a=(3，1)，b=(-2，5)，则3a-2b=（）。

  A(2，7)

  B(13，-7)

  C(2，-7)

  D(13，13)

• 16. 设集合M={2}，N={1，2}，S={1，2，4}，则(M∪N)∩S是（）。

  A{1}

  B{1，2}

  C{4}

  D{1，2，4}

• 17. 设数列{b_n}为等比数列，其中b₃=3，b₅=12，则b₄=（）。

  A15/2

  B6

  C9

  D无法确定

• 1. 已知α、β为锐角，cos(α+β)=12/13，cos(2α+β)=3/5，则cosα=（）。

• 2. 小明5次考试的成绩分别为63、a、50、70、65，已知这5次考试的平均成绩为60，则方差=（）。

• 3. 任选一个不大于20的正整数，它恰好是3的整数倍的概率是（）。

• 4. 函数y=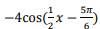的最小正周期是（）。

• 1. 已知椭圆
  （Ⅰ）求C的方程；
  （Ⅱ）设C上一点P的横坐标为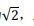F₁、F₂为C的左、右焦点，求△PF₁F₂的面积。

• 2. 已知二次函数 f(x)=x²+bx+c的图像过点P(1，0)，并且对于任意实数x，有f(1+x)=f(1-x)，求函数f(x)的最值。

• 3. 已知△ABC中，A=60°，AB=AC=2，求:
  （1）BC；
  （2）△ABC的面积。

• 4. 设S_n为数列{a_n}的前n项和，S_n=3/2(a_n-1)(n∈N₊)，数列{b_n}的通项公式为b_n=4n+3(n∈N₊)。
  (Ⅰ)求数列｛an｝的通项公式；
  (Ⅱ)若di∈{a1，a2，…，an，…}∩{b1，b2，…，bn，…}(i=1，2，…，n，…)，则称数列{dn}为数列{an}与{bn}的公共项，将数列{an}与{bn}的公共项按它们在原数列中的先后顺序排成一个新的数列(dn)，证明{dn}的通项公式为dn=3²ⁿ⁺¹(n∈N)。