2024年成考高起点理科数学全真模拟卷(五)

• 1. 已知直线l₁与l₂的夹角是( )

  A45°

  B60°

  C120°

  D150°

• 2. 设那么复数Z对应的点的集合表示的图形为( )

  A圆

  B椭圆

  C抛物线

  D双曲线

• 3. 当圆锥的侧面积和底面积的比值是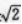时，圆锥轴截面的顶角是（ ）

  A45°

  B60°

  C90°

  D120°

• 4. 下列函数中，最小正周期为π的偶函数是（ ）

  Ay=sinx

  B

  C

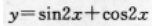
  D

• 5. 设直线的参数方程为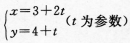则此直线在y轴上的截距是（　　）

  A5

  B-5

  C5/2

  D-5/2

• 6. 直线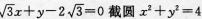所得的劣弧所对的圆心角为（）。

  Aπ/6

  Bπ/4

  Cπ/3

  Dπ/2

• 7. 已知复数z=a+bi，其中a,b∈R，且b≠0，则(　　)。

  A｜z^2｜≠｜z｜²=z²

  B｜z²｜=｜z｜²=z²

  C｜z²｜=｜z｜²≠z²

  D｜z²｜=z²≠｜z｜²

• 8. 把点A(-2，3)平移向量a=(1，-2)。则对应点A’的坐标为(　　)。

  A(-1，1)

  B(1，-1)

  C(-1，-1)

  D(1，1)

• 9. 5名高中毕业生报考3所院校，每人只能报一所院校，则有(　　)种不同的报名方法。

  A

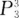
  B5³

  C3⁵

  D

• 10. 下列函数的周期是丌的是(　　)。

  Aƒ(x)=cos²2x-sin²2x

  Bƒ(x)=2sin4x

  Cƒ(x)=sinxcosx

  Dƒ(x)=4sinx

• 11. 若函数f(x)是奇函数，则函数F(x)=f(x)*sin(3π/2-x)的奇偶性是（）。

  A奇函数

  B偶函数

  C非奇非偶函数

  D既是奇函数.又是偶函数

• 12. 已知α、β为锐角，cosα>sinβ，则（）。

  A

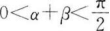
  B

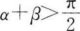
  C

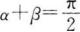
  D

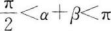
• 13. 若函数ƒ(x)的定义域为[0,1],则ƒ(cosx)的定义域为（）。

  A[0，1]

  B(-∞,+∞)

  C[-π/2，π/2]

  D[2kπ-π/2，2kπ+π/2](k∈Z)

• 14. 在等差数列中{a_n}中，若a₁+a₂=2，a₃+a₄=10，则等差数列中{a_n}的公差d为（）。

  A1

  B2

  C3

  D4

• 15. 下列函数中在实数域上是单调递增的是（）。

  A

  B

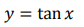
  C

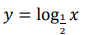
  D

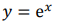
• 16. 直三棱柱的每个侧面的面积为5，底面积是10，全面积是（）。

  A15

  B20

  C25

  D35

• 17. 设全集U={1，2，3，4}，集合M={3，4}，则CUM=（）

  A{2，3}

  B{2，4}

  C{1，2}

  D{1，4}

• 1. 已知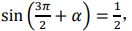则cosα=（）。

• 2. 曲线y=e^x+x在点(0,1)处的切线方程为（）。

• 3. 已知A(-1,-1)，B(3,7)两点，则线段AB的垂直平分线方程为（）。

• 4. 设离散型随机变量ζ的分布列如下表所示，那么ζ的期望等于（）。
  

• 1. 在正四棱柱ABCD-A'B'C'D'中，向量DA=a，向量DC=b，向量DD'=c，
  

• 2. A、B、C是直线L上的三点，P是这条直线外一点，已知AB=BC=a，∠APB=90°，∠BPC=45°。求：(Ⅰ)∠PAB的正弦；
  (Ⅱ）线段PB的长；
  (Ⅲ)P点到直线L的距离

• 3. 正三棱柱ABC—A'B'C'，底面边长为a，侧棱长为h。
  (I)求点A到△A'BC所在平面的距离d；
  (Ⅱ)在满足d=1的上述正三棱柱中，求侧面积的最小值。

• 4. 设函数
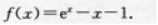
  (I)求f(χ)的单调区间；
  (Ⅱ)求f(χ)的极值。