2022年成考高起点每日一练《数学(理)》10月2日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:952
试卷答案:有
试卷介绍: 2022年成考高起点每日一练《数学(理)》10月2日专为备考2022年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 过抛物线C:y2=4x的焦点作aT轴的垂线,交C于A,B两点,则|AB|=()。
A2
B4
C
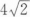
D8
-
2. 已知平面向量a=(1,t),b=(-1,2),若a+mb平行于向量(-2,1),则
A2t-3m+1=0
B2t+3m+1=0
C2t-3m-1=0
D2t+3m-1=0
-
3. 某学校为新生开设了4门选修课程,规定每位新生至少要选其中3门,则一位新生不同的选课方案共()。
A7种
B4种
C5种
D6种
-
4. f(x)为偶函数,在(0,+∞)上为减函数,若f(1/2)>0>f(√3),则方程f(x)=0的根的个数是()。
A2
B2或1
C3
D2或3
-
1.

-
2. A、B、C是直线L上的三点,P是这条直线外一点,已知AB=BC=a,∠APB=90°,∠BPC=45°。求:(Ⅰ)∠PAB的正弦;
(Ⅱ)线段PB的长;
(Ⅲ)P点到直线L的距离
-
3. 已知数列{an}的前n项和
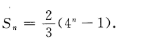 (1)求{an}的通项公式; (2)若ak=128,求k。
(1)求{an}的通项公式; (2)若ak=128,求k。
-
4. 过点(1,-2)且与直线3x+y-1=0垂直的直线方程为.
-
1. 若平面向量a=(x,1),&=(1,-2),且a//b,则x=______.
-
2.
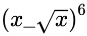 的展开式中,含x4项的系数是().
的展开式中,含x4项的系数是().
相关试卷
-
2024年成考高起点每日一练《数学(理)》4月23日354人做过
-
2024年成考高起点每日一练《数学(理)》4月24日585人做过
-
2024年成考高起点每日一练《数学(理)》4月25日376人做过
-
2024年成考高起点每日一练《数学(理)》4月26日1351人做过
-
2024年成考高起点每日一练《数学(理)》4月27日129人做过
-
2024年成考高起点每日一练《数学(理)》4月28日300人做过
-
2024年成考高起点每日一练《数学(理)》4月29日398人做过
-
2024年成考高起点每日一练《数学(理)》4月30日1526人做过
-
2024年成考高起点每日一练《数学(理)》5月1日1891人做过
-
2024年成考高起点每日一练《数学(理)》5月2日556人做过
相关题库