2022年成考高起点每日一练《数学(理)》10月3日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:1624
试卷答案:有
试卷介绍: 2022年成考高起点每日一练《数学(理)》10月3日专为备考2022年数学(理)考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 已知sinα<0且tanα<0,则α是()。
A第一象限角
B第二象限角
C第三象限角
D第四象限角
-
2. 已知点A(4,1),B(2,3),则线段AB的垂直平分线方程为( )
Ax-y+1=0
Bx+y-5=0
Cx-y-1=0
Dx-2y+1=0
-
3. 设甲:函数:y=kx+6的图像过点(1,1), 乙:k+b=1, 则
A甲是乙的充分必要条件
B甲是乙的必要条件,但不是乙的充分条件
C甲是乙的充分条件,但不是乙的必要条件
D甲不是乙的充分条件,也不是乙的必要条件
-
4.
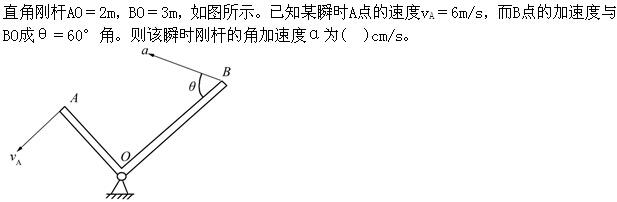
A3
B
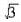
C
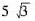
D

-
1. 设函数f(x)=x3-9/2x2+6x+20。(Ⅰ)求f(x)的单调区间,并说明它在各区间的单调性;
(Ⅱ)求f(x)的极值。
-
2. 建筑一个容积为8000m3,深为6m的长方体蓄水池,池壁每m2的造价为15元,池底每m2的造价为30元。(Ⅰ)把总造价y(元)表示为长x(m)的函数;
(Ⅱ)求函数的定义域。
-
3. 设直线y=x+1是曲线y=x3+3x2+4x+a的切线,求切点坐标和a的值.
-
4.
 (Ⅰ)求(Ⅱ)求C的离心率.
(Ⅰ)求(Ⅱ)求C的离心率.
-
1. 各棱长都为2的正四棱锥的体积为_______
-
2. 设正三角形的一个顶点在原点,且关于x轴对称,另外两个顶点在抛物线y2=2√3上,则此三角形的边长为( )。
相关试卷
-
2024年成考高起点每日一练《数学(理)》4月23日354人做过
-
2024年成考高起点每日一练《数学(理)》4月24日585人做过
-
2024年成考高起点每日一练《数学(理)》4月25日376人做过
-
2024年成考高起点每日一练《数学(理)》4月26日1351人做过
-
2024年成考高起点每日一练《数学(理)》4月27日129人做过
-
2024年成考高起点每日一练《数学(理)》4月28日300人做过
-
2024年成考高起点每日一练《数学(理)》4月29日398人做过
-
2024年成考高起点每日一练《数学(理)》4月30日1526人做过
-
2024年成考高起点每日一练《数学(理)》5月1日1891人做过
-
2024年成考高起点每日一练《数学(理)》5月2日556人做过
相关题库