2017下半年教师资格证考试《初中数学》真题及答案

• 1.

  A0

  B1

  C2

  D3

• 2. 当x→x0时，与x-x0叫。是等价无穷小的为()。

  Asin(x-x0)

  Bex-x0

  C(x-x0)2

  DIn|x-x0|

• 3. 下列四个级数中发散的是()。

• 4. 下列关于椭圆的论述，正确的是()。

  A平面内到两个定点的距离之和等于常数的动点轨迹是椭圆

  B平面内到定点和定直线距离之比小于 1 的动点轨迹是椭圆

  C从椭圆的一个焦点出发的射线，经椭圆反射后通过椭圆另一个焦点

  D平面与圆柱面的截线是椭圆

• 5. 下列多项式为二次型的是()。

• 6. 已知随机变量X服从正态分布N(μ，σ2)，设随机变量Y=2X，那么Y服从的分布是()。

  AN(2μ，2σ2)

  BN(4μ，4σ2)

  CN(2μ，4σ2)

  DN(μ，σ2)

• 7. “矩形”和“菱形”概念之间的关系是()。

  A同一关系

  B交叉关系

  C属种关系

  D矛盾关系

• 8. 下列图形不是中心对称图形的是（ ）。

  A线段

  B正五边形

  C平行四边形

  D椭圆

• 1. 将平面曲线y=x2分别绕y轴和x轴旋转一周，所得旋转曲面分别记作S1和S2。(1)在空间直角坐标系中，分别写出曲面S1和S2的方程；
  (2)求平面y=4与曲面S1。所围成的立体的体积。

• 2. 据统计，在参加某类职业资格考试的考生中，有60％是本专业考生，有40％是非本专业考生，其中本专业考生的通过率是85％，非本专业的考生通过率是50％。某位考生通过了考试，求该考生是本专业考生的概率。

• 3. 在平面有界区域内，由连续曲线C围成一个封闭图形。证明：存在实数ξ使直线y=x+ξ平分该图形的面积。

• 4. 给出“平行四边形”和“实数”的定义，并说明它们的定义方式。

• 5. 《义务教育数学课程标准(2011年版)》设置了部分选学内容，以韦达定理为例简述设置选学内容的意义。

• 1. 在线性空间R³中，已知向量a₁=(1，2，1)，a₂=(2，1，4)，a₃=(0，-3，2)，记V₁={λa₁+μa₂|λ，μ∈R}，V₂={ka₃|k∈R}。令V₃={t₁η₁+t₂η₂|t₁，t₂∈R，η₁∈V₁，η₂∈V₂}。
  (1)求子空间V₃的维数；
  (2)求子空间V₃的一组标准正交基。

• 1. 数学的产生与发展过程蕴含着丰富的数学文化。(1)以“勾股定理”教学为例，说明在数学教学中如何渗透数学文化；
  (2)阐述数学文化对学生数学学习的作用。

• 1. 案例：某学校的初二年级数学备课组针对“一次函数”，拟对“兴趣班”的学生上一次拓展课，经过讨论，拟定了如下教学目标：
  ①进一步理解一次函数解析式y=kx+b(k≠0)中参数的含义；②探索两个一次函数图像的位置关系。
  为了落实教学目标②，针对参数k，甲、乙两位老师给出了不同的教学思路：
  【教师甲】
  先出示问题：一次函数图像是直线，两个一次函数表示的直线平行时，它们对应的一次函数解析式中参数k有什么特点呢?
  然后。给出一般结论：若函数y=k1x+b1(k1≠0)，y=kg+b2(k2≠0)表示的两条直线平行，则有k1=k2。接着通过具体实例，让学生体会参数k的含义。
  【教师乙】
  让学生在同一坐标系下，作一次函数图像，在此过程中体会k的含义。如，将学生分两组，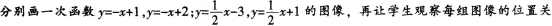
  
  系，从而体会参数k的含义。
  问题：
  (1)对该备课组拟定的教学目标进行评析；
  (2)分析甲、乙两位教师教学思路的特点。

• 1. 在学习了平行四边形、三角形的中位线定理后，某教师设计了一节习题课的教学目标：①进一步理解三角形中位线定理、平行四边形的判定定理；②能综合运用三角形中位线定理、平行四边形的判定定理等知识解决问题；③提高发现和提出数学问题的能力。
  他的教学过程设计中包含了下面的一道例题：
  如图1，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点。
  问题一求证：四边形EFGH是平行四边形；
  问题二如何改变问题中的条件．才能分别得到一个菱形、矩形、正方形?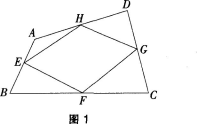
  
  
  针对上述材料，完成下列任务：
  (1)结合该教师的教学目标，分析该例题的设计意图；
  (2)类比上述例题中的问题二，设计一个新问题，使之符合教学目标③的要求；
  (3)设计该例题的简要教学流程，并给出解题后的小结提纲。