2023年高职单招每日一练《数学》6月8日
考试总分:10分
考试类型:模拟试题
作答时间:60分钟
已答人数:333
试卷答案:有
试卷介绍: 2023年高职单招每日一练《数学》6月8日专为备考2023年数学考生准备,帮助考生通过每日坚持练习,逐步提升考试成绩。
试卷预览
-
1. 设a,b为实数,则“b=3”是“a(b-3)=0”的充分不必要条件.
A对
B错
-
2. 已知集合A={-1,0,1,2},B={x|x<0},则A∩B={-1,0}.
A对
B错
-
1. 若函数f(x)= logax(0<a<1)在区间[a,2a]上的最大值是最小值的3倍,则a等于( )
A
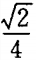
B

C
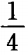
D
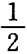
-
2. 已知双曲线的方程为
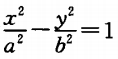 ,点A、B在双曲线的右支上,线段A B 经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则∆ABF1的周长为()。
,点A、B在双曲线的右支上,线段A B 经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则∆ABF1的周长为()。A2a+2m
B4a+2m
Ca+m
D2a+4m
-
1. 已知两直线
 ,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
,当m为何值时,l1与l2: (1)相交;(2)平行;(3)重合.
-
2. 已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
-
1. 若
 ,则x=().
,则x=().
-
2. 若直线x+y+a=0(其中a为常数)经过圆x2+y2-2x+4y-6=0的圆心,则a的值是()
-
1. 已知角α的终边过点P(-8m,-6sin 30°),且
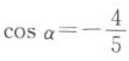 ,求m的值.
,求m的值.
-
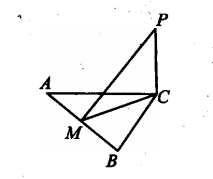
2. 如图∆ABC中,AC=8,∠BAC=60°,PC⊥平面ABC,PC=4,M是AB边上的一个动点,求PM的最小值.
相关试卷
-
2023年高职单招每日一练《数学》6月24日1721人做过
-
2023年高职单招每日一练《数学》6月25日427人做过
-
2023年高职单招每日一练《数学》6月26日228人做过
-
2023年高职单招每日一练《数学》6月27日428人做过
-
2023年高职单招每日一练《数学》6月28日1961人做过
-
2023年高职单招每日一练《数学》6月29日571人做过
-
2023年高职单招每日一练《数学》6月30日1497人做过
-
2023年高职单招每日一练《数学》7月1日1090人做过
-
2023年高职单招每日一练《数学》7月2日1215人做过
-
2023年高职单招每日一练《数学》7月3日1458人做过
相关题库