已知系统的微分方程为:,则传递函数为:/ananas/latex/p/1950325
查看答案
相关试题
换一换


已知系统的微分方程为:,则传递函数为:/ananas/latex/p/1950325
答案
传递函数与系统微分方程二者之间可以
答案
惯性环节的微分方程为( ),传递函数为( )。
A.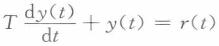 B.
B.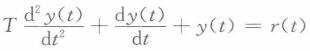 C.
C.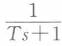 D.
D.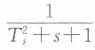
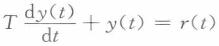 B.
B.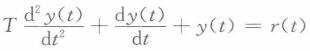 C.
C.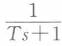 D.
D.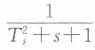
答案
传递函数与系统微分方程二者之间( ? ?)互相转换。
答案
微分方程阶数从传递函数中看不出来
答案
系统的频率特性可以通过系统的微分方程、传递函数、实验3种方法得到。()
A.正确 B.错误
答案
传递函数和微分方程都是系统或环节动态特性的数学模型表达式,不同的是传递函数则在域内表征输入与输出关系()
A.时间(t) B.微积分 C.复变量 S D.矢量
答案
在自动控制系统中,常用的数学模型有微分方程、传递函数、状态方程、传递矩阵、结构框图和信号流图等。()
A.是 B.否
答案
惯性环节的微分方程为Tc(t)+c(t)=r(t),其中T为时间常数,则其传递函数G(s)为( )。
A.1/(Ts+1) B.Ts+1 C.1/(T+s) D.T+s
答案
设积分环节和理想微分环节的微分方程分别为c"(t)= r(t)和c(t)=r""(t),则其传递函数分别为()。
A.G(s)=s和G(s)=s B.G(s)=1/s和G(s)=1/s C.G(s)=s和G(s)=1/s D.G(s)=1/s和G(s)=s
答案
热门试题
设积分环节和理想微分环节的微分方程分别为c′(t)=r(t)和c(t)=r′,则其传递函数分别为( )。
()拉氏变换能够把描述系统状态的传递函数方便地转换为系统的微分方程,并由此可用传递函数的零、极点分布,频率特性等间接地分析和设计控制系统
二阶环节的微分方程为T2c″(t)+2ξTc′(t)+c(t)=r(t),则其传递函数G(s)为( )。
已知y0是微分方程y″+py′+qy=0的解,y1是微分方程y″+py′+qy=f(x)(f(x)≠0)的解,则下列函数中是微分方程y″+py′+qy=f(x)的解的是( )。
单位负反馈系统的开环传递函数为G(s),则其闭环系统的前向传递函数与: 反馈传递函数相同|开环传递函数相同|误差传递函数相同|闭环传递函数相同
含 有未知函数的 或 的方程叫微分方程;微分方程的解一般分为 和
理想微分环节的传递函数为()。
离散系统差分方程,则脉冲传递函数为/ananas/latex/p/445201
由于稳态误差与系统开环传递函数中所含微分环节的数量密切相关,所以将系统按开环传递函数所含微分环节的个数进行分类。()
时变控制系统的微分方程或差分方程的系数是的函数
微分方程中所出现的未知函数的最高阶导数的阶数,叫做微分方程的阶()
微分方程分为常微分方程和偏微分方程两类
已知y是关于x的函数,则微分方程y2dx-(1-x)dy=0是()
第一章1.经典控制理论中,系统的“数学模型”是用微分方程、传递函数、动态结构图等来描述的,这种描述又常称为系统的“外部描述”
微分环节和积分环节的传递函数( )。
理想微分环节的传递函数为Ts。()
利用ode45()函数计算高阶微分方程的解时,必须先把高阶微分方程转化为一阶微分方程组的形式
系统微分方程式的系数与自变量有关,则为非线性微分方程,由非线性微分方程描述的系统称为非线性系统。()
若微分方程的解中含有独立的任意常数的个数与该微分方程的()相同,则该解叫作微分方程的通解.
系统微分方程的通解



 使用微信扫一扫登录
使用微信扫一扫登录