若微分方程的解中含有独立的任意常数的个数与该微分方程的()相同,则该解叫作微分方程的通解.
查看答案
相关试题
换一换


若微分方程的解中含有独立的任意常数的个数与该微分方程的()相同,则该解叫作微分方程的通解.
答案
微分方程的含有任意常数的解是该微分方程的通解。
A.正确 B.错误
答案
微分方程的含有任意常数的解是该微分方程的通解()
答案
若f(x)使常微分方程两端恒等,则f(x)称为常微分方程的解
答案
微分方程的通解是()(C1、C2为任意常数)
A.lnx+C B.ln(x+C C.C2+ln D.C2-ln
答案
函数:(:为任意常数)是微分方程y”-y’-2y=0的()
A.通解 B.特解 C.不是解 D.解,既不是通解又不是特解
答案
微分方程分为常微分方程和偏微分方程两类
答案
设C是任意常数,则下列以y=Cex为解的二阶微分方程是()
A.y”=0 B.y”-3y'-4y=0 C.y”-4y'+3y=0 D.y”+4y'+3y=0
答案
含 有未知函数的 或 的方程叫微分方程;微分方程的解一般分为 和
答案
微分方程ydx+(x-y)dy=0的通解是:(c为任意常数)
A. B.
B. C.
C.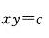 D.
D.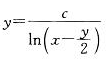
 B.
B. C.
C.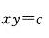 D.
D.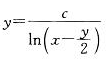
答案
热门试题
下列微分方程是线性微分方程的是()。
利用ode45()函数计算高阶微分方程的解时,必须先把高阶微分方程转化为一阶微分方程组的形式
微分方程是 阶微分方程 /ananas/latex/p/268588
сложная система дифференциальных уравнений: 复杂的微分方程|复杂的微分方程组|复杂的方程组|简单的微分方程组
已知微分方程y"+p(x)y = q(x)[q(x)≠0]有两个不同的特解y1(x), y2(x),C为任意常数,则该微分方程的通解是:
已知微分方程y"+p(x)y=q(x)[q(x)≠0]有两个不同的特解:y1(x),y2(x),则该微分方程的通解是:(c为任意常数)
n阶线性齐次微分方程基本解组中解的个数恰好是()个
(2008)微分方程y″=(y′)2的通解是:(c1,c2为任意常数)()
(2008)微分方程y″=(y′)2的通解是:(c1,c2为任意常数)()
微分方程yn=x+sinx的通解是(c1 ,c2为任意常数)()
已知y0是微分方程y″+py′+qy=0的解,y1是微分方程y″+py′+qy=f(x)(f(x)≠0)的解,则下列函数中是微分方程y″+py′+qy=f(x)的解的是( )。
(2012)已知微分方程y′+p+(x)y=q(x)[q(x)≠0]有两个不同的特解y1(x),y2(x),则该微分方程的通解是:(c为任意常数)()
在下列微分方程中,以函数y=C1e^-x+C2e^4x(C1,C2为任意常数)为通解的微分方程是( )。
解微分方程 : (x+y)dx+xdy=0
微分方程的通解包含了所有的解
微分方程y"-4y=6的通解是(c1,c2为任意常数):
微分方程y′′-4y=4的通解是(C1,C2为任意常数):
微分方程y″-4y=4的通解是( )。(c1,c2为任意常数)
系统微分方程式的系数与自变量有关,则为非线性微分方程,由非线性微分方程描述的系统称为非线性系统。()
已知r1=3,r2=-3是微分方程y"+Py'+qy=0(p和q是常数)的特征方程的两个根,则该微分方程为()



 使用微信扫一扫登录
使用微信扫一扫登录