相关试题
换一换


若对数函数的图像经过点(27,3),则其解析式为 ( )。
A. B.
B. C.
C.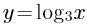 D.
D.
 B.
B. C.
C.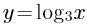 D.
D.
答案
若对数函数的图像过点(4,2),则该对数函数的解析式为().
A.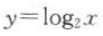 B.
B.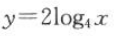 C.
C.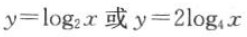 D.不确定
D.不确定
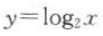 B.
B.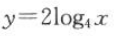 C.
C.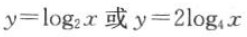 D.不确定
D.不确定 答案
若指数函数的图像经过点(3,27),则其解析式为 ( )。
A.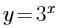 B.
B.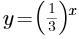 C.
C.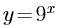 D.
D.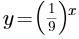
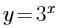 B.
B.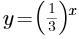 C.
C.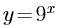 D.
D.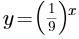
答案
若指数函数的图像经过点(3,27),则其解析式是( )。
A.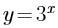 B.
B.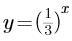 C.
C.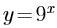 D.
D.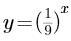
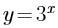 B.
B.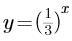 C.
C.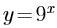 D.
D.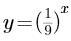
答案
已知函数f(χ)=ax2+b的图像经过点(1,2),且其反函数f-1(χ)的图像经过点(3,0),则函数f(χ)的解析式是()。
A.f(χ)=1/2x2+3/2 B.f(χ)=-χ2+3 C.f(χ)=3χ2+2 D.f(χ)=χ2+3
答案
已知函数ƒ(x)=ax2+b的图像经过点(1,2),且其反函数ƒ-1(x)的图像经过点(3,0),则函数ƒ(x)的解析式是( )。
A.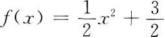 B.ƒ(x)=-x2+3 C.ƒ(x)=3x2+2 D.ƒ(x)=x2+3
B.ƒ(x)=-x2+3 C.ƒ(x)=3x2+2 D.ƒ(x)=x2+3
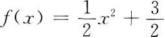 B.ƒ(x)=-x2+3 C.ƒ(x)=3x2+2 D.ƒ(x)=x2+3
B.ƒ(x)=-x2+3 C.ƒ(x)=3x2+2 D.ƒ(x)=x2+3 答案
已知f(x)=ax2+b的图像经过点(1,2)且其反函数f-1(x)图像经过点(3,0),则函数f(x)的解析式是()。
A.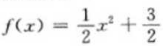 B.f(x)=-x2+3 C.f(x)=3x2+2 D.f(x)=x2+3
B.f(x)=-x2+3 C.f(x)=3x2+2 D.f(x)=x2+3
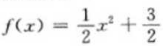 B.f(x)=-x2+3 C.f(x)=3x2+2 D.f(x)=x2+3
B.f(x)=-x2+3 C.f(x)=3x2+2 D.f(x)=x2+3 答案
某函数的图像经过点(1,1)和点(-1,-1),则它的解析式不可能是( )。
A.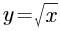 B.
B.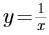 C.
C.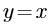 D.
D.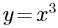
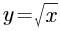 B.
B.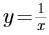 C.
C.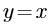 D.
D.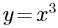
答案
幂函数的原函数一定是: 对数函数|幂函数|指数函数|指数函数或对数函数
答案
某函数的图像经过点(-1,-1)和(1,1),则它的解析式不可能是().
A.y=x B.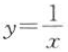 C.
C. D.
D.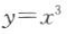
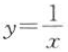 C.
C. D.
D.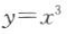
答案
热门试题
下列函数为对数函数的是( )。
下列函数是对数函数的是( )。
若函数f(x)=ax+b的图像经过点(1,3),其反函数的图像经过点(2,0),求a,b的值.
函数y=f(x)存在反函数,若f(2)=-3,则函数y=f-1(x)的图像经过点( )
若函数y=2x-1+3的反函数的图像经过点P,则点P的坐标是()。
若函数 f(x)=2x+b 的图像经过点(0,3),则b的值是( )。
下列运算是自然对数函数和指数函数的运算指令()
已知二次函数经过(-1,0),(1,0),(2,3)三点,则这个函数的解析式为()
说明平方根函数,指数函数和对数函数的BASIC语言表示法
已知一次函数y=2x+b的图像经过点(-2,1),则该图像也经过点( )
已知一次函数y-2x+b的图像经过点(-2,1),则该图像也经过点 ( )
设函数y=k/x的图像经过点(2,-2),则k=
下列运算()不是自然对数函数和指数函数的运算指令(SIEMENS系统)
已知函数y=ax²+bx+c的图像经过点A(-5,0),B(0,-5)两点,它的对称轴为直线x=5,求二次函数的解析式。
若函数f(x)=log2(5x+1),则其反函数y=f-1(x)的图像过点( )
对数函数y=lg(x+4)的定义域为[-4,+∞)
一次函数的图象经过点A(-2,-,且与直线y=2x-3平行,则此函数的解析式为()
若一次函数 y=kx-3 的图像经过点(2,5),则 k 的值等于是( )。
如果函数y—z+b的图像经过点(1,7),则b= ( )
下列运算()不是自然对数函数和指数函数的运算指令(FANUC系统、华中系统)。



 使用微信扫一扫登录
使用微信扫一扫登录