设f(x)在(-∞,+∞)内有定义,且对任意x,y∈(-∞,+∞)(x≠y)有|f(x)-f(y)|<|x-y|,证明:F(x)=f(x)+x在(-∞,+∞)内单调增加.
查看答案
相关试题
换一换


设f(x)在(-∞,+∞)内有定义,且对任意x,y∈(-∞,+∞)(x≠y)有|f(x)-f(y)|<|x-y|,证明:F(x)=f(x)+x在(-∞,+∞)内单调增加.
答案
设函数f(x,y)在点(0,0)的某邻域内有定义,且fx(0,0)=3,fy(0,0)=-1,则有( ).
A.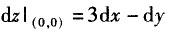 B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.
B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.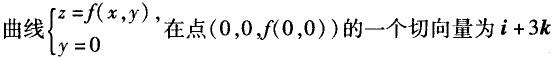 D.
D.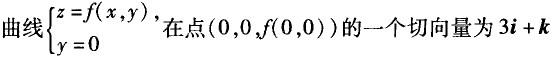
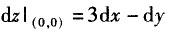 B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.
B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.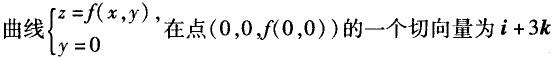 D.
D.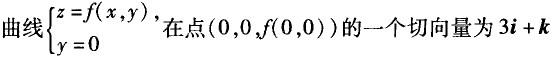
答案
设对任意的,总有,且,则为( )。
答案
设f(x)在(一∞,+∞)内有定义,且存在常数k与α>1,使|f(x1)-f(x2)|≤k|x1-x2|α对任意x1、x2成立.证明:f(x)=c (-∞
答案
设f(x)在(-∞,+∞)内有定义,且存在常数k与α>1,使|f(x1)-f(x2)|≤k|x1-x2|α对任意x1、x2成立。证明:f(x)=c(-∞<x<+∞,c为常数)。
答案
设函数f(x,y)在点(0,0)附近有定义,且fx′(0,0)=3,fy′(0,0)=1,则( )。
A.dz|(0,0)=3dx+dy B.曲面z=f(x,y)在点(0,0,f(0,0))的法向量为(3,1,1) C.曲线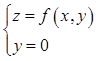 在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线
在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线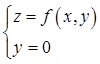 在点(0,0,f(0,0))的法向量为(3,0,1)
在点(0,0,f(0,0))的法向量为(3,0,1)
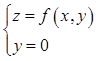 在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线
在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线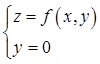 在点(0,0,f(0,0))的法向量为(3,0,1)
在点(0,0,f(0,0))的法向量为(3,0,1) 答案
设任意集合A和B,A~B,当且仅当有f:A→B为( )
答案
设A为n阶正定矩阵,证明:对任意的可逆矩阵P,P^TAP为正定矩阵.
答案
设f(x)和φ(x)在(-∞,+∞)内有定义,f(x)为连续函数,且f(x)≠0,φ(x)有间断点,则( ).
A.必有间断点 B.必有间断点 C.必有间断点 D.必有间断点
答案
设f(x)和φ(x)在(-∞,+∞)内有定义,f(x)为连续函数,且f(x)≠0,φ(x)有间断点,则( )。
A.φ[f(x)]必有间断点 B.[φ(x)]^2必有间断点 C.f[φ(x)]必有间断点 D.φ(x)/f(x)必有间断点
答案
热门试题
设(A,≤)为格,对任意a,b,c∈A,则有a∨(b∧c)≤(a∨b)∧(a∨c)且(a∧b)∨(a∧c)≤a∧(b∨c)
设X是连续型随机变量,P{|X|≤1}=1。证明:对任意0<ε≤1,有P{|X|≥ε}≥E(X2)-ε2。
设X是连续性随机变量,P{|X|≤1}=1.证明:对任意0<ε≤1,有P{|X|≥ε}≥E(X2)-ε2.
设函数y=f(x)在(0,+∞)内有界且可导,则( )。
设函数y=f(x)在(0,+∞)内有界且可导,则( )。
设A、B为任意随机事件,证明:P(AB)=1-P(A(_))-P(B(_))+P(A(_)B(_))。
设随机变量X的密度函数为f(x),且f(-x)=f(x),F(x)是X的分布函数,则对任意实数a有( )。
设A为n阶方阵,若对任意n维向量x(→)=(x1,x2,…,xn)T都有Ax(→)=0。证明:A=0。
已知false是定义在false上的不恒为零的函数,且对任意的false都满足false
设随机变量X的概率密度为f(x),且f(x)=f(-x),F(x)是X的分布函数,则对任意实数a,有[ ]
设A,B为n阶矩阵,且r(A)+r(B)
设域F的特征为2,对任意的a,b∈F,有(a+b)^2=
设f(x)在[a,b]上二阶可导,且恒有f"(x)<0,证明:若方程f(x)=0在(a,b)内有根,则最多有两个根.
设A为n阶方阵,若对任意n维向量X=(x1,x2,…,xn)T都有AX=0.证明:A=0.
设ƒ(x)在(a,b)内有定义,x0∈(a,b),则下列命题中正确的是( )
设随机变量X的概率密度和分布函数分别是f(x)和F(x),且f(x)=f(-x),则对任意实数a,有F(-a)=()
设在[0,+∞]上函数f(x)有连续导数,且f′(x)≥k>0,f(0)
设在[0,+∞]上函数f(x)有连续导数,且f′(x)≥k>0,f(0)<0,证明:在(0,+∞]内有且仅有一个零点。
设f(x)在[a,+∞)上连续,在(a,+∞)内可导,且f′(x)>k>0(k为常数),又f(a)<0,证明方程f(x)=0在(a,a-f(a)/k)内有唯一实根。
设f(x)是定义在[-a,a]上的任意函数,则下列答案中哪个函数不是偶函数?()



 使用微信扫一扫登录
使用微信扫一扫登录