设f(x),f′(x)在[a,b]上连续,f″(x)在(a,b)内存在,f(a)=f(b)=0,且存在c∈(a,b)使f(c)>0。证明:必∃ξ∈(a,b)使f″(ξ)<0。
查看答案
相关试题
换一换


设f(x),f′(x)在[a,b]上连续,f″(x)在(a,b)内存在,f(a)=f(b)=0,且存在c∈(a,b)使f(c)>0。证明:必∃ξ∈(a,b)使f″(ξ)<0。
答案
设函数f(x)在[a,b]上连续且f(x)>0,则
A.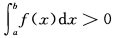 B.
B.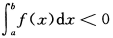 C.
C.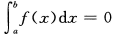 D.
D.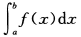 的符号无法确定
的符号无法确定
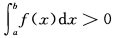 B.
B.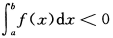 C.
C.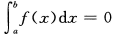 D.
D.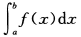 的符号无法确定
的符号无法确定 答案
设函数f(x)在[a,b]上连续且f(x)>0,则( )
A.见图A B.见图B C.见图C D.见图D E.见图E
答案
设函数f(x)在[a,b]上连续且f(x)>0,则()
A.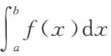 >0 B.
>0 B.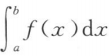 <0 C.
<0 C.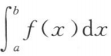 =0 D.
=0 D.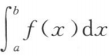 的符号无法确定
的符号无法确定
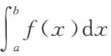 >0 B.
>0 B.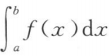 <0 C.
<0 C.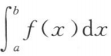 =0 D.
=0 D.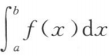 的符号无法确定
的符号无法确定 答案
设函数f(t)在[0,+∞)上连续,
且满足方程,求f(t).
答案
设y=f(x)在[0,1]上连续,且f(0)>0,f(1)<0,则下列正确的是()
A.y=f(x)在[0,1]上可能无界 B.y=f(r)在[0,1]上未必有最小值 C.y=f(x)在[0,1]上未必有最大值 D.方程f(x)=0在(0,1)内至少有一个实根
答案
设函数f(x)在(0,1)上可导且在[0,1]上连续,且f'(x)>0,f(0)<0,f(1)>0,则f(x)在(0,1)内()。
A.至少有一个零点 B.有且仅有一个零点 C.没有零点 D.零点的个数不能确定
答案
设函数f(x)连续,且f′(0)>0,则存在δ>0,使得( )。
A.f(x)在(0,δ)内单调增加 B.f(x)在(-δ,0)内单调减少 C.对任意的x∈(0,δ)有f(x)>f(0) D.对任意的x∈(-δ,0)有f(x)>f(0)
答案
设f′(x)在[a,b]上连续,且f′(a)>0,f′(b)<0,则下列结论中错误的是( )。
A.至少存在一点x0∈(a,b),使得f(x0)>f(a) B.至少存在一点x0∈(a,b),使得f(x0)>f(b) C.至少存在一点x0∈(a,b),使得f′(x0)=0 D.至少存在一点x0∈(a,b),使得f(x0)=0
答案
设ƒ(x)在[0,2a]上连续,且ƒ(0)=ƒ(2a),证明:在[0,a]上至少存在一个ξ,使得ƒ(ξ)=ƒ(ξ+a)。
答案
热门试题
设f(x)在(-a,a)是连续的偶函数,且当0()
设f(x)在(-a,a)是连续的偶函数,且当0
设f(x)在(-a,a)是连续的偶函数,且当0()
设函数f(t)连续,t∈[-a,a],f(t)>0,且则在[-a,a]内必有()
设偶函数f(x)具有二阶连续导数,且f″(0)≠0,则x=0( )。
设f(x)在闭区间[0,c]上连续,其导数f′(x)在开区间(0,c)内存在且单调减少,f(0)=0,试应用拉格朗日中值定理证明不等式f(a+b)≤f(a)+f(b)其中a,b满足条件0≤a≤b≤a+b≤c.
设函数f(x)在[0,1]上连续,在(0,1)内二阶可导,且f′(x)<0,f"(x)<0,则下列结论成立的是()
设f(x)在内连续,且f(x)>0,证明函数在(0,+∞)内为单调增函数。
设f(x)在(-a,a)是连续的偶函数,且当0<x<a时,f(x)<f(0),则有结论( )。
设f(x)是(-a,a)是连续的偶函数,且当0<x<a时,f(x)<f(0),则有结论()
设函数f(x)在[0,1]上连续,在(0,1)内可导,且f(0)=0,k为正整数,求证:存在一点ξ∈(0,1),使得ξf′(ξ)+kf(ξ)=f′(ξ).
设f(x)在[a,+∞)上连续,在(a,+∞)内可导,且f′(x)>k>0(k为常数),又f(a)<0,证明方程f(x)=0在(a,a-f(a)/k)内有唯一实根。
设f(x)在[0,π]上连续,在(0,π)内可导,证明:必∃ξ∈(0,π),使f′(ξ)+3f(ξ)cotξ=0。
设f(x)在[0,2]上连续,在(0,2)内可导,且f(0)+f(1)=4,f(2)=2,试证明必存在一点ξ∈(0,2),使f′(ξ)=0.
设函数f(x)在区间[0,2]上连续,在区间(0,2)内可导,且f(0)=f(2)=f(1)=2,证明:至少存在一点ξ∈(0,2),使得f′(ξ)=ξ.
设f(x)在[a,b]上连续,在(a,b)内可导,且f(a)·f(b)>0,f(a)·f[(a+b)/2]<0。试证:对任意实数k,∃ξ∈(a,b),使得f′(ξ)=kf(ξ)。
设函数f(x)在点x=O的某邻域内具有连续的二阶导数,且f′(0)=f″(0)=0,则( )。
设在[0,+∞]上函数f(x)有连续导数,且f′(x)≥k>0,f(0)
设在[0,+∞]上函数f(x)有连续导数,且f′(x)≥k>0,f(0)<0,证明:在(0,+∞]内有且仅有一个零点。
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f(x)>0,f(x)>0,则在(-∞,0)内必有( )。



 使用微信扫一扫登录
使用微信扫一扫登录