设函数f(x)对任意x均满足f(x+1)=af(x),且f′(0)=b,其中a,b为非零常数,则()
A. f(x)在x=1处不可导
B. f(x)在x=1处可导,且f′(1)=a
C. f(x)在x=1处可导,且f′(1)=b
D. f(x)在x=1处可导,且f′(1)=ab
查看答案
相关试题
换一换


设函数f(x)对任意x均满足f(x+1)=af(x),且f′(0)=b,其中a,b为非零常数,则()
A.f(x)在x=1处不可导 B.f(x)在x=1处可导,且f′(1)=a C.f(x)在x=1处可导,且f′(1)=b D.f(x)在x=1处可导,且f′(1)=ab
答案
设函数f(x)对任意x均满足等式f(1+x)=af(x),且有f'(0)=b,其中a,b为不相等的非零常数,则( )
A.f(x)在x=1处不可导 B.f(x)在x=1处可导,且f'(1)=a C.f(x)在x=1处可导,且f'(1)=b D.f(x)在x=1处可导,且f'(1)=ab
答案
设函数y=f(x)在(-∞,+∞)上可导,且对任意实数a、b均满足f(a+b)=eaf(b)+ebf(a),又知f′(0)=e,试求f(x)及f′(x)。
答案
设函数f(x,y)在点(0,0)附近有定义,且fx′(0,0)=3,fy′(0,0)=1,则( )。
A.dz|(0,0)=3dx+dy B.曲面z=f(x,y)在点(0,0,f(0,0))的法向量为(3,1,1) C.曲线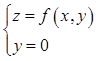 在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线
在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线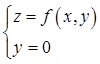 在点(0,0,f(0,0))的法向量为(3,0,1)
在点(0,0,f(0,0))的法向量为(3,0,1)
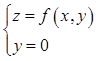 在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线
在点(0,0,f(0,0))的法向量为(1,0,3) D.曲线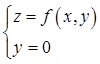 在点(0,0,f(0,0))的法向量为(3,0,1)
在点(0,0,f(0,0))的法向量为(3,0,1) 答案
设函数f(x,y)在点(0,0)的某邻域内有定义,且fx(0,0)=3,fy(0,0)=-1,则有( ).
A.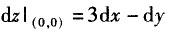 B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.
B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.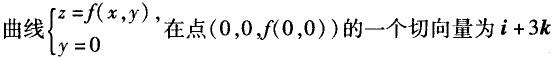 D.
D.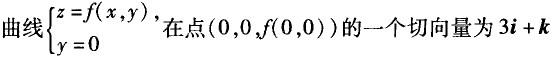
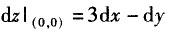 B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.
B.曲面z=f(x,y)在点(0,0,f(0,0))的一个法向量为3i-j+k C.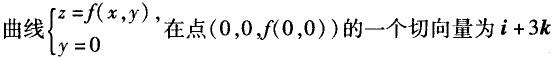 D.
D.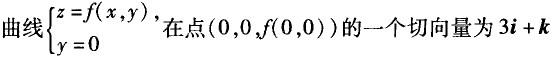
答案
设函数f(x)在x=0可导且f(0)=1,又设f(x)满足函数方程f(x+1)=2f(x),求f′(n),其中n是整数。
答案
设f(x,y,z)=exyz2,其中z=z(x,y)是由x+y+z+xyz=0确定的隐函数,则fx′(0,1,-1)=____。
答案
若函数f(x)对任意实数x1、x2均满足关系式f(x1+x2)=f(x1)f(x2)。且f′(0)=2,则必有( )
A.f(0)=0 B.f(0)=2 C.f(0)=1 D.f(0)=-1
答案
已知函数f(x,y)满足fxy″=2(y+1)ex,fx′(x,0)=(x+1)ex,f(0,y)=y2+2y,求f(x,y)的极值。
答案
设f(x),g(x)具有任意阶导数,且满足f″(x)+f′(x)g(x)+f(x)x=ex-1,f(0)=1,f′(0)=0。则( )。
A.f(0)=1为f(x)的极小值 B.f(0)=1为f(x)的极大值 C.(0,f(0))为曲线y=f(x)的拐点 D.由g(x)才能确定f(x)的极值或拐点
答案
热门试题
设函数f(x)满足关系式f″(x)+[f′(x)]2=x,且f′(0)=0,则( )。
设函数f(x)满足f(x+Δx)-f(x)=2xf(x)Δx+ο(Δx)(Δx→0),且f(0)=2,则f(1)=
设函数f(x)满足f”(x)-3f'(x)+2f(x)=0,且在x=0处取得极值1,求函数f(x)的表达式.
设函数f(x)在[a,b]上连续且f(x)>0,则
设函数f(x)在[a,b]上连续且f(x)>0,则( )
设函数f(x)在[a,b]上连续且f(x)>0,则()
设函数f(x)在[a,b]上连续,满足f([a,b])∈[a,b]。证明:存在x0,∈[a,b],使得f(x0)=x0。
设函数f(x)满足关系式f"(x)+[f′(x)]2=-2,且f′(0)=0则()
设函数f(x)在区间[1,+∞)内二阶可导,且满足条件f(1)=f′(1)=0,x>1时f″(x)<0,则g(x)=f(x)/x在(1,+∞)内( )。
设函数f(x)满足f'(sin2x)=cos2x,且f(0)=0,则f(x)=()
设函数f (x)在(a, b)内可微,且≠0,则f(x)在(a,b)内()
设F1(x),F2(x)都是分布函数,a>0,b>0是两个常数,且a+b=1。试证明:F(x)=aF1(x)+bF2(x)也是分布函数。
已知函数f(x)的定义域为(-∞,+∞),对任意的x,y,有f(x+y))+f(x-y)=2f(x)f(y)成立,且f(0)≠0.求证:
(1)f(0)=1;
(2)函数f(x)是偶函数.
若f(x)为奇函数,且对任意实数x恒有f(x+3)-f(x-1)=0,则f(2)=
设函数f(x)在x=1处可导,且f"(1)=0,若f"(1)>0,则f(1)是()
设函数f(x)在(0,1)上可导且在[0,1]上连续,且f'(x)>0,f(0)<0,f(1)>0,则f(x)在(0,1)内()。
设f(x)是R上的可导函数,且f(x)>0。若f?(x)-3x2f(x)=0,且f(0)=1,求f(x)。
设 f(x)是 R 上的可导函数,且 f(x)>0。若 f"(x)-3x---2f(x)=0,且 f(0)=1,求 f(x)。
设f(x)是[0,1]上的可导函数,且f′(x)有界。证明:存在M>0,使得对于任意x1,x2∈[0,1],有|f(x1)-f(x2)|≤M|x1-x2|。
若函数f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),则在(a,b)内满足f ′(x0)=0的点x0( )。



 使用微信扫一扫登录
使用微信扫一扫登录