设a为N阶可逆矩阵,则( ).
A. 若AB=CB,则A=C:
B.  C. A总可以经过初等变换化为单位矩阵E:
D. 以上都不对
C. A总可以经过初等变换化为单位矩阵E:
D. 以上都不对

查看答案
相关试题
换一换


设a为N阶可逆矩阵,则( ).
A.若AB=CB,则A=C: B. C.A总可以经过初等变换化为单位矩阵E: D.以上都不对
C.A总可以经过初等变换化为单位矩阵E: D.以上都不对
 C.A总可以经过初等变换化为单位矩阵E: D.以上都不对
C.A总可以经过初等变换化为单位矩阵E: D.以上都不对 答案
设a为N阶可逆矩阵,则( ).
A.若AB=CB,则a=C: B. C.A总可以经过初等变换化为单位矩阵E: D.以上都不对
C.A总可以经过初等变换化为单位矩阵E: D.以上都不对
 C.A总可以经过初等变换化为单位矩阵E: D.以上都不对
C.A总可以经过初等变换化为单位矩阵E: D.以上都不对 答案
设A,B都是n阶可逆矩阵,则
答案
设A,B为同阶可逆矩阵,则( )。
A.AB=BA B.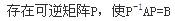 C.
C.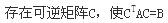 D.存在可逆矩阵P和Q,使PAQ=B
D.存在可逆矩阵P和Q,使PAQ=B
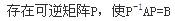 C.
C.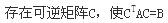 D.存在可逆矩阵P和Q,使PAQ=B
D.存在可逆矩阵P和Q,使PAQ=B 答案
设A、B均为n阶可逆矩阵,则必有()
答案
设A为n阶可逆矩阵,则(-A)的伴随矩阵(-A)n等于( )。
A.-An B.An C.(-1)nAn D.(-1)n-1An
答案
设A,B都是N阶矩阵,且存在可逆矩阵P,使得AP=B,则().
A.A,B合同 B.A,B相似 C.方程组AX=0与BX=0同解 D.r(A)=r(B)
答案
设矩阵A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )。
A.矩阵C的行向量组与矩阵A的行向量组等价 B.矩阵C的列向量组与矩阵A的列向量组等价 C.矩阵C的行向量组与矩阵B的行向量组等价 D.矩阵C的列向量组与矩阵B的列向量组等价
答案
设A,B都是N阶矩阵,且存在可逆矩阵P,使得AP=B,则()
A.A,B合同 B.A,B相似 C.方程组AX=0与BX=0同解 D.r(A)=r()
答案
设矩阵A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )
A.矩阵C的行向量组与矩阵A的行向量组等价 B.矩阵C的列向量组与矩阵A的列向量组等价 C.矩阵C的行向量组与矩阵B的行向量组等价 D.矩阵C的行向量组与矩阵B的列向量组等价
答案
热门试题
设n阶可逆矩阵A满足2|A|=|kA|,k>0,则k=____.
设A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )。
设A,B,C均为n阶矩阵,若AB=C,且B可逆,则
设A,B都是n阶矩阵。若有可逆矩阵P使得P1AP=B,则称矩阵A与矩阵B( )。
设A,B都是n阶可逆矩阵,则下述结论中不正确的是()。
设A是m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r,矩阵B=AC的秩为r1,则( )。
设A是m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r,矩阵B=AC的秩为r1,则( )。
设A,N,A+B,A-1+B-1均为n阶可逆矩阵,则(A-1+B-1)=()
设A为n阶正定矩阵,证明:对任意的可逆矩阵P,P^TAP为正定矩阵.
设A是m×N阶矩阵,B是n×m阶矩阵,则().
设A是m×N阶矩阵,B是n×m阶矩阵,则()
设3阶矩阵A,B满足AB=A+B.证明A-E可逆.
中国大学MOOC: 设A与B均为n阶可逆矩阵,则只用初等行变换可把A变为B
中国大学MOOC: 设A与B均为n阶可逆矩阵,则只用初等行变换可把A变为B
设N阶矩阵A与对角矩阵合同,则A是().
已知A2-3A-E=0,设A为n阶矩阵,E为n阶单位矩阵若A可逆,试用A表示;若A不可逆,说明理由。
设A为n(n≥2)阶可逆矩阵,交换A的第1行与第2行得矩阵B,,分别为A,B的伴随矩阵,则()
设A为n(n≥2)阶可逆矩阵,交换A的第1行与第2行得矩阵B,分别为A,B的伴随矩阵,则( )。
设A,B,A+B,A-1+ B-1均为n阶可逆矩阵,则(A-1+ B-1)-1=( )。
设A,B,A+B,A-1+ B-1均为n阶可逆矩阵,则(A-1+ B-1)-1=( )。



 使用微信扫一扫登录
使用微信扫一扫登录