一圆柱底面积为S,侧面展开图为正方形,则这个圆柱的全面积为( )
A. 4πS
B. (1+4π)S
C. (2+4π)S
D. (3+4π)S
查看答案
相关试题
换一换


一圆柱底面积为S,侧面展开图为正方形,则这个圆柱的全面积为( )
A.4πS B.(1+4π)S C.(2+4π)S D.(3+4π)S
答案
圆柱底面积为S,侧面展开图形为正方形,则这个圆柱的全面积是()。
A.4πS B.(1+4π)S C.(2+4π)S D.(3+4π)S
答案
圆柱底面积为S,侧面展开图形为正方形,则这个圆柱的全面积是( ).
A.4πS B.( l+4π)S C.(2+4π)S D.(3+4π)S
答案
圆柱底面积为S,侧面展开图形为正方形,则这个圆柱的全面积是()
A.4πS B.(1+4π)S C.(2+4π)S D.(3+4π)S
答案
一个圆柱的侧面展开图是正方形这个圆柱的高和底面半径的比值是()
A.兀 B.2兀 C.3兀 D.2
答案
一个圆柱的侧面展开图是正方形,那么它的侧面积是下底面积的( )倍
A.2 B.4 C.4π D.π E.2π
答案
一个圆柱的侧面展开图是一个正方形,这个圆柱的底面半径与高的比是()
A.1:2π B.1:4π C.1:π
答案
一个圆柱的侧面展开图是一个正方形,这个圆柱的表面积与侧面积的比是().
A. B.
B. C.
C.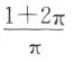 D.
D.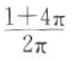
 B.
B. C.
C.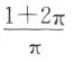 D.
D.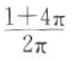
答案
一个圆柱的侧面展开图是一个边长为62.8厘米的正方形,这个圆柱的侧面积是()平方厘米,它的表面积是()平方厘米
A.251.2,4571.84 B.3943.84,4571.84 C.4571.844
答案
如果把圆柱的侧面沿高展开后得到一个正方形,那么圆柱的高等于()
A.底面直径 B.底面直径的л倍 C.底面半径的л倍
答案
热门试题
若一圆柱的底面直径与高都等于一球的直径,则该球的体积等于这个圆柱的()
圆柱底面周长和高相等时,沿着它的一条高剪开,侧面是一个正方形()
已知圆柱的轴截面是面积为4的正方形,则圆柱体的体积是()
已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是()
已知轴截面是正方形的圆柱的高与球的直径相等,则圆柱的全面积与球的表面积的比是( )
如图中的正方形、圆柱和圆锥底面积相等,高也相等,下面哪句话是正确的?( )
图形面积相等的两个图,如:圆和正方形,在视觉上感到正方形的面积()圆的面积。
一个正方体的底面积和一个圆柱体的底面积相等,且侧面积相等,求正方体与圆柱体的体积比.
若圆锥的表面积为S,且它的侧面展开图是一个半圆,则这个圆锥的底面圆直径为().
在正方形里面画一个最大的圆,正方形面积和圆的面积的比是()
一圆柱体的底面直径和高均为2,则其体积为()
图形面积相等的圆、正方形,给人的感觉正方形大而圆面积小。
圆柱的侧面展开图是( )
一个正方形与这个正方形内最大的圆的周长的比是()。(π≈3.14)
已知一个正方形的内切圆面积为36π平方厘米,则这个正方形的面积为()平方厘米
一平面图形绕一圆柱做螺旋运动时,则得到一()
计算题:一圆柱试样直径为10mm,试计算其截面积?
一圆锥的侧面展开图是圆心角为120°,半径为6cm的扇形,则此圆锤的侧面积为()
由一圆柱和一棱柱所构成的立体称为()
由一圆柱和一棱柱所构成的立体称为()



 使用微信扫一扫登录
使用微信扫一扫登录