一个圆柱的侧面展开图是一个正方形,这个圆柱的底面半径与高的比是()
A. 1:2π
B. 1:4π
C. 1:π
查看答案
相关试题
换一换


一个圆柱的侧面展开图是一个正方形,这个圆柱的底面半径与高的比是()
A.1:2π B.1:4π C.1:π
答案
一个圆柱的侧面展开图是正方形这个圆柱的高和底面半径的比值是()
A.兀 B.2兀 C.3兀 D.2
答案
一个圆柱的侧面展开图是一个正方形,这个圆柱的表面积与侧面积的比是().
A. B.
B. C.
C.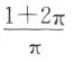 D.
D.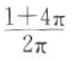
 B.
B. C.
C.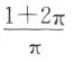 D.
D.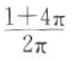
答案
一个圆柱的侧面展开图是正方形,那么它的侧面积是下底面积的( )倍
A.2 B.4 C.4π D.π E.2π
答案
一个圆柱的侧面展开图是一个边长为62.8厘米的正方形,这个圆柱的侧面积是()平方厘米,它的表面积是()平方厘米
A.251.2,4571.84 B.3943.84,4571.84 C.4571.844
答案
圆柱底面积为S,侧面展开图形为正方形,则这个圆柱的全面积是()。
A.4πS B.(1+4π)S C.(2+4π)S D.(3+4π)S
答案
圆柱底面积为S,侧面展开图形为正方形,则这个圆柱的全面积是( ).
A.4πS B.( l+4π)S C.(2+4π)S D.(3+4π)S
答案
圆柱底面积为S,侧面展开图形为正方形,则这个圆柱的全面积是()
A.4πS B.(1+4π)S C.(2+4π)S D.(3+4π)S
答案
一圆柱底面积为S,侧面展开图为正方形,则这个圆柱的全面积为( )
A.4πS B.(1+4π)S C.(2+4π)S D.(3+4π)S
答案
如果把圆柱的侧面沿高展开后得到一个正方形,那么圆柱的高等于()
A.底面直径 B.底面直径的л倍 C.底面半径的л倍
答案
热门试题
圆柱底面周长和高相等时,沿着它的一条高剪开,侧面是一个正方形()
一个正方体的底面积和一个圆柱体的底面积相等,且侧面积相等,求正方体与圆柱体的体积比.
圆柱的侧面展开得到一个长方形,它的长相当于圆柱的()
圆柱的侧面展开得到一个长方形,它的宽相当于圆柱的()
底面周长和高相等的圆柱,侧面沿高展开后得到一个()
:我们知道,一个正方形可以剪成4个小正方形,那么一个正方形能否剪成9个正方形,能否剪成11个正方形(大小不一定要相同)( )
我们知道,一个正方形可以剪成4个小正方形,那么一个正方形能否剪成11个正方形,能否剪成13个正方形(大小不一定相同):
一个正方形与这个正方形内最大的圆的周长的比是()。(π≈3.14)
一个正方形的边长是a厘米,当a=10时,这个正方形的面积是()平方厘米。
要拼成一个大正方形至少需要()个小正方形
一个圆柱和一个圆锥的体积相等,底面半径的比是2:1,那么圆柱和圆锥的高的比是()
下面是同一个圆柱的展开图。说一说每个图是怎样展开的,画出每个侧面图的高。
一个正方形能分成 4 个正方形 能分成 11 个正方形吗 大小不一定相等?
用一根绳子围了一个长40厘米的正方形,这个正方形的边长是多少厘米()
搭一个正方形需要4根小棒,搭a个正方形需要()根小棒。
用两个同样大小的正方形可以拼成一个大的正方形()
一个圆柱的底面半径是3厘米,高是5厘米,它的侧面积是()平方厘米
一个半径为1厘米的圆在一个边长为8厘米的正方形内,沿正方形的边与边相切滚动过正方形一周。圆滚动覆盖的总面积为()平方厘米。
一个长方形和一个正方形的周长相等,它们的面积()。
已知一个正方形的内切圆面积为36π平方厘米,则这个正方形的面积为()平方厘米



 使用微信扫一扫登录
使用微信扫一扫登录