相关试题
换一换


已知sinx=2cosx,则tanx=( )。
A.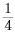 B.
B.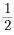 C.2 D.4
C.2 D.4
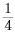 B.
B.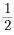 C.2 D.4
C.2 D.4 答案
已知f(x)=sinx+cosx,则f(-x)等于()
A.-sinx+cosx B.sinx-cosx C.-sinx-cosx D.sinx+cosx
答案
∫[(4sinx+3cosx)/(sinx+2cosx)]dx=()
A.2^x-ln|sinx+cosx|+C B.x^2-ln|sinx+cosx|+C C.x^2-ln|sinx+2cosx|+C D.2^x-ln|sinx+2cosx|+C
答案
∫[(4sinx+3cosx)/(sinx+2cosx)]dx=____。
答案
∫[(4sinx+3cosx)/(sinx+2cosx)]dx=( )。
A.2^x-ln|sinx+cosx|+C B.x^2-ln|sinx+cosx|+ C.x^2-ln|sinx+2cosx|+C D.2^x-ln|sinx+2cosx|+C
答案
设f′(cosx)=sinx,则f(cosx)等于()
A.-cosx+c B.cosx+c C.1/2(sin2x/2-x)+c D.1/2(2sin2x-x)+c
答案
设Y=sinx+COSx,则dy等于().
A.(cosx+sinx)dx B.(-cosx+sinx)dx C.(cosx-sinx)dx D.(-cosx-sinx)dx
答案
对于函数y=sin(tanx)-tan(sinx)(0≤x≤π),x=π/2是( )。
A.连续点 B.第一类间断点 C.可去间断点 D.第二类间断点
答案
若sinx=a,cosx=b,那么sin2x等于()
A.2ab B.ab/2 C.ab D.a+b
答案
y=sinx+cosx
答案
热门试题
已知f’(x)=tanx2,且f(0)=1,则f(x)等于().
∫[(x+sinx)/(1+cosx)]dx=()
∫[(x+sinx)/(1+cosx)]dx=( )。
已知f′(2+cosx)=sin2x+tan2x,则f(x)=____。
方程y"=sinx+cosx的通解为()。
当x→0时,tanx-sinx是x3的().
求出两多项式函数P(x)、Q(x),使得下面等式成立: ∫[(2x4-1)cosx+(8x3-x2-1)sinx]dx=P(x)cosx+Q(x)sinx+C
f(x)=|cosx|+|sinx|的最小正周期是()
已知函数f(x)=tanx,则下列说法正确的是()
设ƒ(tanx)=tan2x,则ƒ(2)=()。
求微分方程y”-y=e2x(sinx-cosx)的通解.
当x→0时,sinx·cosx与x比较是()。
函数f(x)=√3sinx-cosx的值域为()
曲线y=(x+4sinx)/(5x-2cosx)的水平渐近线方程为____。
已知sinx=a-4, 则a的取值范围( )。
已知cosx=3-a, 则a的取值范围是( )。
在区间[0,2π]上,曲线:y=sinx与y=cosx之间所围图形的面积是:
在区间(0,2π)上,曲线y=sinx与y=cosx之间所围图形的面积是( )。
已知cosx=α,求sin(x+3π/2)=()
\(\int e^xsinx{dx}=\frac 12e^x(sinx-cosx)\)



 使用微信扫一扫登录
使用微信扫一扫登录