下列各式成立的是()
A. a-b+c=a-(b+c)
B. a+b-c=a-(b-c)
C. a-b-c=a-(b+c)
D. a-b+c-d=(a+c)-(b-d)
查看答案
相关试题
换一换


下列各式成立的是()
A.a-b+c=a-(b+c) B.a+b-c=a-(b-c) C.a-b-c=a-(b+c) D.a-b+c-d=(a+c)-(b-d)
答案
下列各式成立的是( )。
A.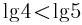 B.
B.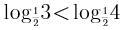 C.
C.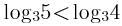 D.
D.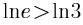
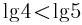 B.
B.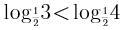 C.
C.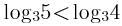 D.
D.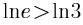
答案
下列各式中,不成立的是()。
A.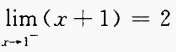 B.
B.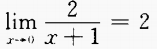 C.
C.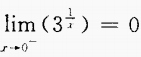 D.
D.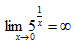
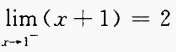 B.
B.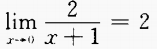 C.
C.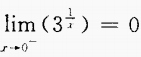 D.
D.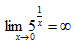
答案
下列各式中,一定能成立的是()
A.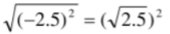 B.
B.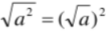 C.
C. D.
D.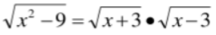
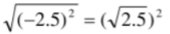 B.
B.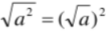 C.
C. D.
D.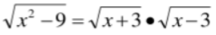
答案
设函数f(x)=logax,且f(4)=2,则下列各式成立的是
A.f(3)<O B.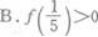 C.f(5)<f(3) D.f(3)<f(5)
C.f(5)<f(3) D.f(3)<f(5)
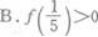 C.f(5)<f(3) D.f(3)<f(5)
C.f(5)<f(3) D.f(3)<f(5) 答案
设X~N(0,1),则下列各式成立的有()
A.P(X>a)=P(X≥a)=φ(a) B.P(a≤X≤b)=φ(b)-φ(a) C.P(X|≤a)=2φ(a)-1 D.φ(-a)=-φ(a) E.φ(-a)=2 φ(a)
答案
设x~N(0,1),则下列各式成立的有( )。
A.P(X>a)=P(X≥a)=φ(a) B.P(a≤X≤b)=φ(b)-φ(a) C.P(|X|≤a)=2φ(a)-1 D.φ(-a)=-φ(a) E.φ(-a)=2φ(a)
答案
若C为任意常数,且F’(x)=f(x),则下列各式成立的是()。
A.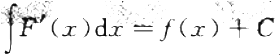 B.
B.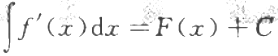 C.
C.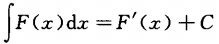 D.
D.
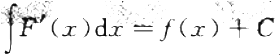 B.
B.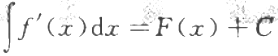 C.
C.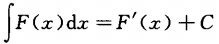 D.
D.
答案
若P(A)>0,P(B)>0,P(A│B)=P(A),则下列各式不成立的是()
A.P(B│A.=PB B.P(A│)=P C.P(AB.=PPB D.A,B互斥
答案
若P(A) >0,F(B) >0,P(A B)=P(A),则下列各式不成立的是:
A.P(B A)=P(B) B.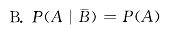 C.P(AB)=P(A)P(B) D.A,B互斥
C.P(AB)=P(A)P(B) D.A,B互斥
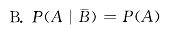 C.P(AB)=P(A)P(B) D.A,B互斥
C.P(AB)=P(A)P(B) D.A,B互斥 答案
热门试题
若P(A)>0,P(B)>0,P(AB)=P(A),则下列各式不成立的是( )。
设f(x)在[a,b]上连续,且a≠-b,则下列各式不成立的是()
(2008)若P(A)>0,P(B)>0,P(A│B)=P(A),则下列各式不成立的是:()
(2008)若P(A)>0,P(B)>0,P(A│B)=P(A),则下列各式不成立的是:()
(2008)若P(A)>0,P(B)>0,P(A│B)=P(A),则下列各式不成立的是:()
设函数f(x)=logax,且f(4)=2,则下列各式成立的是()。
设a,b向量互相平行,但方向相反,且|a|>|b|>0,则下列各式中哪个成立()?
设a,b向量互相平行,但方向相反,且|a|>|b|>0,则下列各式中哪个成立()
若x=1是方程ax2+bx+c=0的解,则下列各式一定成立的是()
如果∫df(x)=∫dg(x),则下列各式中哪一个不一定成立?()
如果∫df(x)=∫dg(x),则下列各式中哪一个不一定成立?
如果∫df(x)=∫dg(x),则下列各式中哪一个不一定成立?()
下列各式正确的是()
下列各式正确的是( )。
下列各式正确的是( )。
下列各式正确的是( )。
下列各式错误的是( )。
已知ƒ(x)是定义域在[-5,5]上的偶函数,且ƒ(3)>ƒ(1),则下列各式一定成立的是()。
A、B为随机事件,满足0<P(A)<1,0<P(B)<1,且P(A-B)=0,则下列各式中成立的是( )。
下列各式计算正确的是()



 使用微信扫一扫登录
使用微信扫一扫登录