设函数f(x)=logax,且f(4)=2,则下列各式成立的是
A. f(3)<O
B. 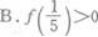 C. f(5)<f(3)
D. f(3)<f(5)
C. f(5)<f(3)
D. f(3)<f(5)
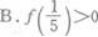
查看答案
相关试题
换一换


设函数f(x)=logax,且f(4)=2,则下列各式成立的是
A.f(3)<O B.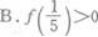 C.f(5)<f(3) D.f(3)<f(5)
C.f(5)<f(3) D.f(3)<f(5)
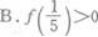 C.f(5)<f(3) D.f(3)<f(5)
C.f(5)<f(3) D.f(3)<f(5) 答案
设函数f(x)=logax,且f(4)=2,则下列各式成立的是()。
A.f(3)<O B.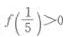 C.f(5)<f(3) D.f(3)<f(5)
C.f(5)<f(3) D.f(3)<f(5)
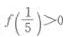 C.f(5)<f(3) D.f(3)<f(5)
C.f(5)<f(3) D.f(3)<f(5) 答案
设f(x)在[a,b]上连续,且a≠-b,则下列各式不成立的是()
A.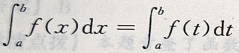 B.
B.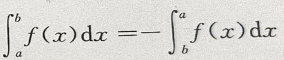 C.
C.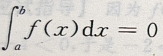 D.
D.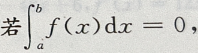 必有f(x)
必有f(x)
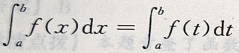 B.
B.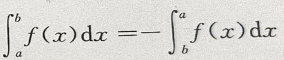 C.
C.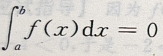 D.
D.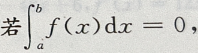 必有f(x)
必有f(x) 答案
若C为任意常数,且F’(x)=f(x),则下列各式成立的是()。
A.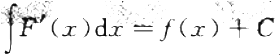 B.
B.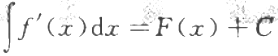 C.
C.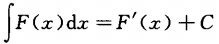 D.
D.
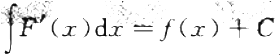 B.
B.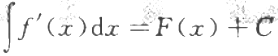 C.
C.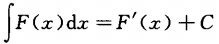 D.
D.
答案
设函数f(x)在区间[a,b]连续且不恒为0,则下列各式不恒为常数的是()。
A.f(b)-f(a) B. C.
C.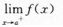 D.
D.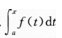
 C.
C.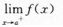 D.
D.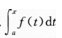
答案
设函数f(x)可导,且f(x)f"(x)>0,则
A.Af(1)>f(-1) B.f(1)|f(-1)| D.|f(1)|
答案
设函数f(x)可导,且f(x)f′(x)>0,则( )。
A.f(1)>f(-1) B.f(1)<f(-1) C.|f(1)|>|f(-1)| D.|f(1)|<|f(-1)|
答案
设a,b向量互相平行,但方向相反,且|a|>|b|>0,则下列各式中哪个成立()?
A.|a+b|=|a|-|b| B.|a+b|>|a|-|b| C.|a+b|
答案
设a,b向量互相平行,但方向相反,且|a|>|b|>0,则下列各式中哪个成立()
A.|a+b|=|a|-|b| B.|a+b|>|a|-|b| C.|a+b|<|a|-|b| D.|a+b|=|a|+|b|
答案
F(x)与G(x)是函数f(x)的两个原函数,则下列各式正确的是
答案
热门试题
设函数f(x)=x+b,且f(2)=3,则f(3)=______。
设函数f(x)=x+b,且f(2)=3,则f(3)=______。
设函数f(x)连续,且f′(0)>0,则存在δ>0,使得( )。
设函数f(x)在[a,b]上连续且f(x)>0,则
设函数f(x)在[a,b]上连续且f(x)>0,则( )
设函数f(x)在[a,b]上连续且f(x)>0,则()
设函数f(x)在[0,1]上连续,在(0,1)内二阶可导,且f′(x)<0,f"(x)<0,则下列结论成立的是()
若f(x)为偶函数,且在(0,+∞)为增函数,则下列不等式成立的是()。
已知函数f(x)为可导函数,且F(x)为f(x)的一个原函数,则下列关系式不成立的是()
设函数f(x)=2ax2-ax,且f(2)=-6,则a=()
设f(x)是[-2,2]上的偶函数,且f′(-1)=3,则f′(1).
设f(x)是[-2,2]上的偶函数,且f'(-1)=3,则f'(1)=()
设f(x)为连续函数,且下列极限都存在,则其中可推出f′(3)存在的是( )。
设函数f(x),g(x)的定义域均为R,且f(x)为奇函数,g(x)为偶函数,则下列说法正确的是()
设X~N(0,1),则下列各式成立的有()
设x~N(0,1),则下列各式成立的有( )。
设f(x)是以7为周期的偶函数,且f(-2)=5,则f(9)=()
设f(x)是以7为周期的偶函数,且f(-2)=5,则f(9)=( )
设f(x)是以7为周期的偶函数,且f(-2)=5,则f(9)=()。
设f(x)为偶函数,且二阶可导,f"(0)≠0,则下列结论正确的是()



 使用微信扫一扫登录
使用微信扫一扫登录