相关试题
换一换


若C为任意常数,且F’(x)=f(x),则下列各式成立的是()。
A.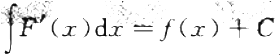 B.
B.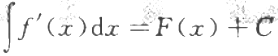 C.
C.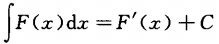 D.
D.
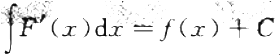 B.
B.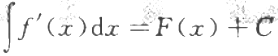 C.
C.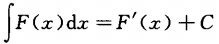 D.
D.
答案
下列各式中正确的是哪一个(c为任意常数)()?
A.f′(3-2x)dx=-(1/2)f(3-2x)+c B.f′(3-2x)dx=-f(3-2x)+c C.f′(3-2x)dx=f(x)+c D.f′(3-2x)dx=(1/2)f(3-2x)+c
答案
若a<b , c<0, 则下列各式正确的是( )。
A.a+c>b+c B.ac<bc C.ac<0 D.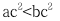
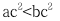
答案
已知a>b,若c是任意实数,则下列不等式中总是成立的是()
A.a+c<b+c B.a-c>b-c C.ac<bc D.ac>bc
答案
若x=1是方程ax2+bx+c=0的解,则下列各式一定成立的是()
A.a+b+c=1 B.a+b+c=0 C.a-b+c=0 D.a-b+c=1
答案
若c为任意常数,则与Ψ描述体系同一状态的波函数是()
A.Ψ* B.Ψ*Ψ C.cΨ* D.c*Ψ
答案
若a>0,且m,n为整数,则下列各式正确的是( )。
A.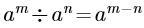 B.
B.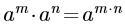 C.
C.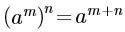 D.
D.
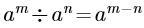 B.
B.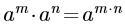 C.
C.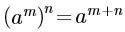 D.
D.
答案
若∫f(x)dx=x3+c,则∫f(cosx)sinxdx等于:(式中c为任意常数)()
A.-cos3x+c B.sin3x+c C.cos3x+c
答案
设函数f(x)=logax,且f(4)=2,则下列各式成立的是
A.f(3)<O B.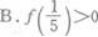 C.f(5)<f(3) D.f(3)<f(5)
C.f(5)<f(3) D.f(3)<f(5)
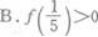 C.f(5)<f(3) D.f(3)<f(5)
C.f(5)<f(3) D.f(3)<f(5) 答案
设f(x)在[a,b]上连续,且a≠-b,则下列各式不成立的是()
A.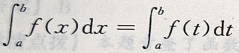 B.
B.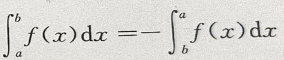 C.
C.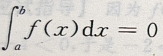 D.
D.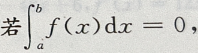 必有f(x)
必有f(x)
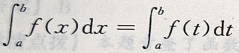 B.
B.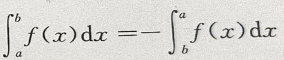 C.
C.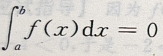 D.
D.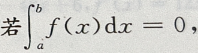 必有f(x)
必有f(x) 答案
热门试题
若P(A) >0,F(B) >0,P(A B)=P(A),则下列各式不成立的是:
若P(A)>0,P(B)>0,P(A│B)=P(A),则下列各式不成立的是()
若P(A)>0,P(B)>0,P(AB)=P(A),则下列各式不成立的是( )。
设函数f(x)=logax,且f(4)=2,则下列各式成立的是()。
(2008)若P(A)>0,P(B)>0,P(A│B)=P(A),则下列各式不成立的是:()
(2008)若P(A)>0,P(B)>0,P(A│B)=P(A),则下列各式不成立的是:()
(2008)若P(A)>0,P(B)>0,P(A│B)=P(A),则下列各式不成立的是:()
若A、B为非零常数,C1、C2为任意常数,则微分方程y″+k2y=cosx的通解应具有形式( )。
设a,b向量互相平行,但方向相反,且|a|>|b|>0,则下列各式中哪个成立()?
设a,b向量互相平行,但方向相反,且|a|>|b|>0,则下列各式中哪个成立()
若a < b ,则下列各式正确的是( )。
若a、b、c、d都是任意实数,则下列命题正确的是( )
设x、y为两个随机变量,a、为任意常数,则下列格式成立的有()
等于( )。(C为任意常数)
已知a>0且a≠1,则下列各式错误的是( )。
若a,b,c∈R,a>b,则下列不等式成立的是().
若a>b,则下列各式一定正确的是( )。
设集合A、B、C为任意集合,若A×B=A×C,则B=C()
设C是任意常数,则下列以y=Cex为解的二阶微分方程是()
.若 A?B 且 B?C,则 A?C。



 使用微信扫一扫登录
使用微信扫一扫登录