请以四边形为属概念,选择不同的概念种差,给出平行四边形的几组定义。
查看答案
相关试题
换一换


请以四边形为属概念,选择不同的概念种差,给出平行四边形的几组定义。
答案
学生已经有“四边形”的概念,现在要学习“平行四边形”,这是一种()。
A.派生类属学习 B.相关类属学习 C.上位学习 D.并列结合学习
答案
设甲:四边形ABCD是平行四边形,乙:四边形ABCD是正方形,则()。
A.甲是乙的充分条件,但不是乙的必要条件 B.甲是乙的必要条件,但不是乙的充分条件 C.甲是乙的充分必要条件 D.甲不是乙的充分条件,也不是乙的必要条件
答案
(2014陕西咸阳)学生已知“平行四边形”这一概念的意义,教师再通过“菱形是四边一样长的平行四边形”这一命题界定菱形,使学生在掌握平行四边形概念基础上学习菱形这一概念,这种学习属于()。
A.派生类属学习 B.总括学习 C.相关类属学习 D.组合学习
答案
平行四边形的()相等
A.四个角 B.四条边 C.对边
答案
学生学习了长方形、正方形、平行四边形后,掌握了“四边形”概念。这种学习是()
A.连锁学习 B.概念学习 C.辨别学习 D.规则学习
答案
下列条件中,能判定四边形ABCD为平行四边形的是()
A.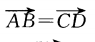 B.
B.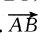
 C.
C.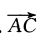
 D.
D.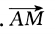
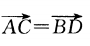
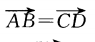 B.
B.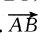
 C.
C.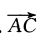
 D.
D.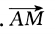
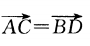
答案
儿童在学习了“平行四边形”这个概念后,再学习“矩形”“菱形”和“正方形”这 些特殊的平行四边形,这属于( )。
A.下位学习 B.上位学习 C.组合学习 D.派生类属学习
答案
学生学习了正方形、长方形、平行四边形后,掌握了“四边形”的概念。这种学习属于( )。
A.辨别学习 B.连锁学习 C.规则学习 D.概念学习
答案
学生学习了长方形、正方形、平行四边形后,掌握了“四边形”的概念。这种学习是( )。
A.连锁学习 B.概念学习 C.辨别学习 D.规则学习
答案
热门试题
一个平行四边形底缩小10倍,高扩大10倍,这个平行四边形的面积()。
平行四边形有()条高。
力的平行四边形公理
平行四边形有()条高
平行四边形是特殊的()
小学生在学习了平行四边形后,再学菱形的概念时便知道“菱形是四条边相等的平行四边形”,这种学习方式属于()
小学生学习了四边形以后,再学习平行四边形。这种学习属于()。
如果一个四边形是中心对称图形,那么这个四边形一定是平行四边形吗?为什么?
设M={平行四边形},N={四边形},P={矩形},则这些集合之间的关系为()
什么是平行四边形法则?
平行四边形:长方形:内角()
《义务教育教学课程标准》关于平行四边形的性质的教学要求是:探索并证明平行四边形的性质定理——平行四边形的对边以及对角相等,请基于该要求,完成下列教学设计任务:(1)设计平行四边形性质的教学目标;(2)设计两种让学生发现平行四边形性质的教学流程;(3)设计平行四边形性质证明的教学流程,使学生领悟证明过程中的教学思想方法
三角形∶平行四边形
三角形:平行四边形()
设命题甲:四边形为菱形,命题乙:四边形为平行四边形,则甲是乙的必要不充分条件。()
用向量的方法证明:对角线互相平分的四边形ABCD是平行四边形.
把一个平行四边形拉成一个长方形,平行四边形的面积()长方形的面积
从平行四边形一条边上的一点到它的对边的(),就是平行四边形的高
平行四边形四条边一定相等()
平行四边形机构为双曲柄机构。



 使用微信扫一扫登录
使用微信扫一扫登录