相关试题
换一换


设函数z=sin(xy),则下列结论正确的是().
A.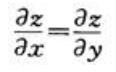 B.
B.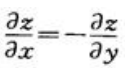 C.
C.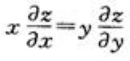 D.
D.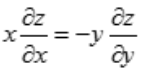
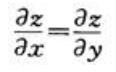 B.
B.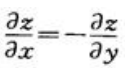 C.
C.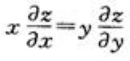 D.
D.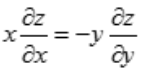
答案
设随机变量X的分布函数为F(x),则下列结论正确的是()。
A.F(x)的定义域为[0,1] B.F(x)是连续函数 C. D.F(x)是不减函数
答案
已知函数y=|x|/x,则下列结论正确的是()。
A.在x=0处有极限 B.在x=0处连续 C.在定义域内连续不可导 D.在定义域内连续可导
答案
设f(x)为偶函数,且二阶可导,f"(0)≠0,则下列结论正确的是()
A.x=0不是f(x)的驻点 B.x=0不是f(x)的极值点 C.x=0是f(x)的极值点 D.(0,f(0))是f(x)的拐点
答案
设a>b,a,b,c∈R,则下列结论正确的是()
A.ac²>bc² B.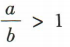 C.a-c>b-c D.a²>b²
C.a-c>b-c D.a²>b²
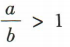 C.a-c>b-c D.a²>b²
C.a-c>b-c D.a²>b² 答案
设A,B皆为n阶矩阵,则下列结论正确的是().
A.AB=O的充分必要条件是A=O或B-O B.AB≠O的充分必要条件是A≠0且B≠0 C.AB=O且r(A)=N,则B=O D.若AB≠0,则|A|≠0或|B|≠0
答案
设ɑ、β均为非零向量,则下面结论正确的是()。
A.ɑⅹβ=0是ɑ与β垂直的充要条件 B.ɑ·β=0是a与β平行的充要条件 C.ɑⅹβ=0是a与β平行的充要条件 D.若ɑ=λβ (βλ是常数),则ɑ×β=0
答案
设、 β均为非零向量,则下面结论正确的是()
A.xβ=0是与β垂直的充要条件 B..β是与β平行的充要条件 C.xβ=0是与β平行的充要条件 D.若=λβ (入是常数),则.β=0
答案
设α、β均为非零向量,则下面结论正确的是( )。
A.α×β=0是α与β垂直的充要条件 B.α·β=0 是α与β平行的充要条件 C.α×β=0是α与β平行的充要条件 D.若α=λβ (λ是常数),则α·β=0
答案
设α、β均为非零向量,则下面结论正确的是()
A.α×β=0是α与β垂直的充要条件 B.α·β=0是α与β平行的充要条件 C.α×β=0是α与β平行的充耍条件 D.若α=λβ(λ是常数),则α·β=0
答案
热门试题
设P(A)=0.8,P(B)=0.7,P(A|B)=0.8,则下列结论正确的是.
设a,b,c, d∈R,且a>b, c>d,则下列结论正确的是( ).
设P(A)=0.8,P(B)=0.7,P(A∣B)=0.8,则下列结论正确的是()
设a,b,c,d∈R,且a>b,c>d,则下列结论正确的是()
设随机变量(X,Y)的分布函数为F(x,y),用它表示概率P(-X
设随机变量(X,Y)的分布函数为F(x,y),用它表示概率P(-X
设数据组为:3.0、3.1、3.3、3.2、3.4、3.2,则下列结论正确的有( )。
设A是n阶矩阵,下列结论正确的是()
设A是n阶矩阵,下列结论正确的是().
已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上为减函数,则下列结论正确的是()
设f(x)在(-a,a)(a>0)上连续,F(x)是f(x)的一个原函数,则当f(x)是奇函数时,下面结论正确的是()。
设f(x)在(-a,a)(a>0)上连续,F(x)是f(x)的一个原函数,则当f(x)是偶函数时,下面结论正确的是()。
设A和B互不相容,且P(A)>0,P(B)>0,则下列结论正确的是()
设A是m×n矩阵,AX=0是AX=b的导出组,则下列结论正确的是( ).
设A是m×n矩阵,AX=0是AX=b的导出组,则下列结论正确的是().
设A和B互不相容,且P(A)>0,P(B)>0,则下列结论正确的是()
设事件A与B互不相容,且P(A)>0,P(B)>0,则下列结论正确的是( )。
反比例函数图象如图所示,下列结论正确的是 ______
设f(t)为连续函数,a是常数,则下列结论中正确的是( )。
若x=x0为函数y=f(x)的极大值点,则下列结论正确的是()



 使用微信扫一扫登录
使用微信扫一扫登录