设函数f(x),g(x)均可微,且同为函数h(x)的原函数,又f(5)=7,g(5)=2,则f(x)-g(x)=().
查看答案
相关试题
换一换


设函数f(x),g(x)均可微,且同为函数h(x)的原函数,又f(5)=7,g(5)=2,则f(x)-g(x)=().
答案
设函数f(x)、g(x)均可微,且同为某函数的原函数,f(1)=3,g(1)=1,则f(x)-g(x)
A.0 B.1 C.2 D.3
答案
设f(x)是连续函数,F(x)是f(x)的原函数,则()。
A.当f(x)是奇函数时,F(x)必是偶函数 B.当f(x)是偶函数时,F(x)必是奇函数 C.当f(x)是周期函数时,F(x)必是周期函数 D.当f(x)是单调增函数时,F(x)必是单调增函数
答案
若函数f(x)在(a,b)内存在原函数,则原函数有()。
A.一个 B.两个 C.无穷多个 D.其他选项都选
答案
设f(x)是连续的偶函数,则其原函数F(x)一定是()
A.偶函数 B.奇函数 C.非奇非偶函数 D.有一个是奇函数
答案
设f(x)的一个原函数是arctanx,则f(x)的导函数是()
A.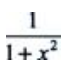 B.
B. C.
C. D.
D.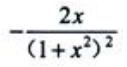
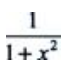 B.
B. C.
C. D.
D.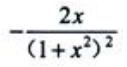
答案
设F(x)为f(x)的一个原函数,且f(x)=xInx,求F(x)。
答案
设F(x)为f(x)的一个原函数,且f(x)=xInx,求F(x)。
答案
设sinx/x为f(x)的一个原函数,且a≠0则∫[f(ax)/a]dx等于( )。
A.sinax/(a3x)+C B.sinax/(a2x)+C C.sinax/(ax)+C D.sinax/x+C
答案
设f(x)的一个原函数为cosx,g(x)的一个原函数为x2,则f[g(x)]等于:()
A.cosx2 B.-sinx2 C.cos2x D.-sin2x
答案
热门试题
函数f(x)的原函数,称为f(x)的不定积分
设F(x)是f(x)的一个原函数,则等于()。
设2x为f(x)的-个原函数,则f(x)=【】
设x是f(x)的一个原函数,则f(x)=()。
设x是f(x)的一个原函数,则f(x)=()。
设f(x)是连续函数,F(x)是f(x)的一个原函数,则下列叙述正确的是()
()是函数f(x)=1/2x的原函数。
若f(x)的导函数是cosx,则函数f(x)有一个原函数是()
已知函数f(x)为可导函数,且F(x)为f(x)的一个原函数,则下列关系式不成立的是()
象函数的原函数f(k)为。/ananas/latex/p/2180598
设f(x)的一个原函数为lnx,则f(x)等于()。
已知f(x)为连续的偶函数,则f(x)的原函数中:
已知f(x)为连续的偶函数,则f(x)的原函数中:
已知f(x)为连续的偶函数,则f(x)的原函数中()
若F(x)是f(x)的一个原函数,G(x)是1/f(x)的一个原函数,且F(x)G(x)=-1,f(0)=1,求f(x)。
设2x为f(x)的一个原函数,则f(x)=【】
设F(z)是f(z)的一个原函数,则∫cosxf(sinx)dx=( )
(2013)已知f(x)为连续的偶函数,则f(x)的原函数中:()
若f(χ)的导函数是sinχ,则f(χ)有一个原函数为( )。
已知象函数F(s)求解原函数f(t)的过程称为拉氏变换。( )



 使用微信扫一扫登录
使用微信扫一扫登录