直线x+2y+1=0与直线y=2x-3垂直。
查看答案
相关试题
换一换


直线x+2y+1=0与直线y=2x-3垂直。
A.对 B.错
答案
过直线x+y+1=0和直线x-2y+4=0的交点,且与直线x+2y-3=0垂直的直线方程是()
A.2x-y+3=0 B.2x-y+5=0 C.x+2γ-4=0 D.2x-y-3=0
答案
已知直线y=ax与直线y=-2x-3垂直,则a的值为()
A.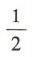 B.
B.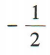 C.-1 D.1
C.-1 D.1
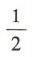 B.
B.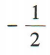 C.-1 D.1
C.-1 D.1 答案
求过直线3x+2y+1=0与2x-3y+5=0的交点,垂直于直线l:6x-2y+5=0的直线方程.
答案
过直线3x+2y+1=0与2x-3y+5=0的交点,且垂直于直线L:6x-2y+5=0的直线方程是( )
A.x-3y-2=0 B.x+3y-2=0 C.x-3y+2=0 D.x+3y+2=0
答案
过直线3x+2y+1=0与2x-3y+5=0的交点,且垂直于直线L:6x-2y+5=0的直线方程是()。
A.x-3y-2=0 B.x+3y-2=0 C.x-3y+2=0 D.x+3y+2=0
答案
下列直线与直线3x-2y=0 垂直的是( ).
A.4x-6y-3=0 B.4x+6y+3=0 C.6x+4y+3=0 D.6x-4y-3=0
答案
经过圆x2+2x+y2=0的圆心,与直线x+y=0垂直的直线方程是( )。
A.x+y+1=0 B.x-y-1=0 C.x+y-1=0 D.x-y+1=0
答案
与直线2x-y+3=0垂直的直线的斜率为( )。
A. B.
B.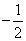 C.-2 D.2
C.-2 D.2
 B.
B.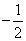 C.-2 D.2
C.-2 D.2 答案
下列直线与直线3x-2y-1=0垂直的是( )。
A.4x-6y-3=0 B.4x+6y+3=0 C.6x+4y+3=0 D.6x-4y-3=0
答案
热门试题
直线y=2x+3与直线y=2x-1的位置关系为?()
直线3x+y-5=0与直线x-3y+5=0垂直。
过直线2x-y+4=0与x-y+5=0的交点,且垂直于直线x-2y=0的直线的方程为()
直线3x+4y-2=0与直线2x+y+2=0的交点坐标是()
直线y=x与直线3x-3y-10=0互相平行。()
经过点A(2,1),与直线2x+y-10=0垂直的直线方程是______
直线x-2y+2=0与直线3x+y-1=0的交点坐标为_____
若直线y-3=2(x+2)与直线y=k(x+6)平行,则k=( )。
直线2x-3y+6=0与直线2x-3y+8=0之间的距离为( )。
求经过直线x+y-3=0,2x-y+8=0交点,且垂直于2x+3y-6=0的直线.
过圆x2+y2-2x-8=0的圆心,且与直线x+2y=0垂直的直线方程是()
若直线y=kx+1与直线2x-y+1=0垂直,则k=()
直线x-2y+3=0与直线2x+y-4=0的交点坐标为(1,2)。
若直线x+ay-3=0与直线2x-y+1=0垂直,则a的值为( )。
直线x+3y-4=0与直线2x-6y+8=0平行。
若直线ax+2y-3=0与x+y-1=0互相垂直,则a=()
直线y=3与直线x=2的交点坐标为(3,2)。
直线3x-2y=0和直线2x+y+1=0的交点坐标为(-2,-3)。
已知直线l1:x-2y+4=0与直线l2:3x+y-2=0相交于P点.(1)求交点P的坐标;(2)求过点P且与直线x-y+3=0垂直的直线l的方程.
直线2x-y+3=0与直线x+2y-1=0的交点坐标是(-1,1)。



 使用微信扫一扫登录
使用微信扫一扫登录